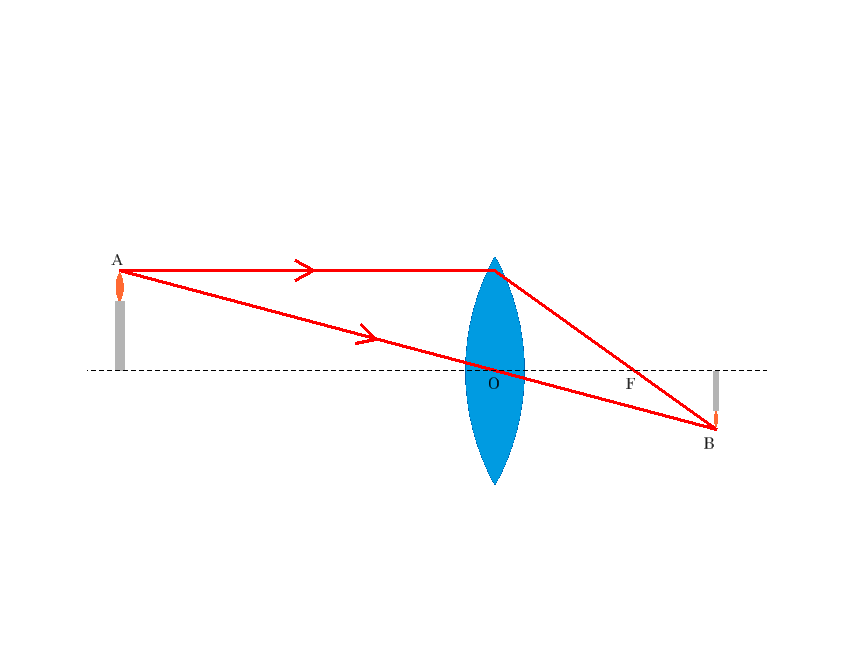
子供のころ、理科の教科書で

こんな図を見た覚えはありませんか？青いのは凸レンズ、Aと書いてあるところには実際にろうそくがあって、Bには実像ができるんですよーとかなんとか。あるいは実験として、Bの場所前後にレンズと平行にスクリーンを置いて観察してみたり。

乱暴にいうとBの場所にフィルム(※1)置いたらカメラのできあがり！ですよね。というのを前置きに、前回の続きです。

 

…

 

前回も見たこの図で

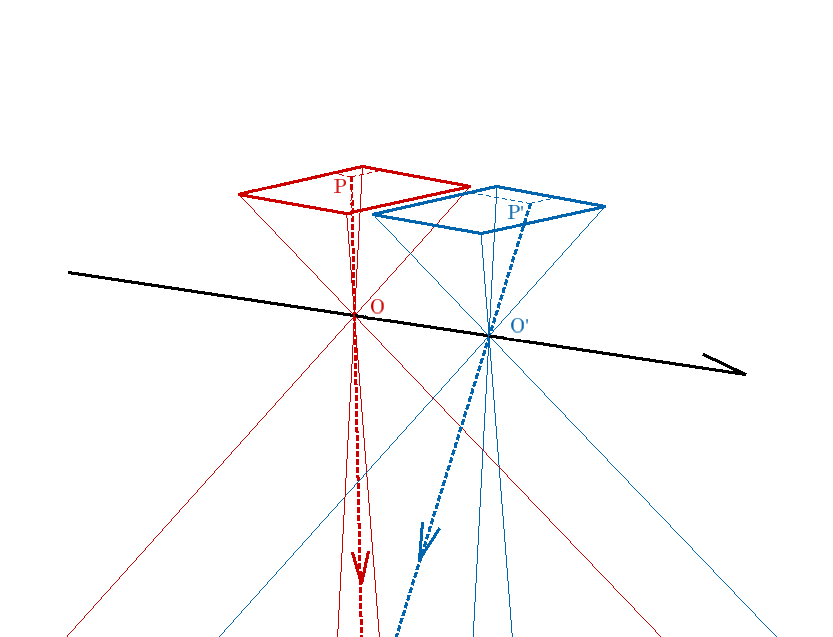
飛行機にはもちろんカメラが積んであります。上の図で飛行機の場所は赤青それぞれ四角錐の頂点になっていますが、カメラが積んであるのはちょうどこの頂点でここから下に向け地上を撮影しています。

さて、カメラを構成する物にはレンズやフィルムがありますが、より細かく見ると、この四角錐の頂点はどちらを表しているでしょうか？百聞は云々、邪魔な飛行機は消してそのあたりを都合よく拡大して考えてみましょう。

 

…

 

 

どーん。

と本当に都合よく、黒い矢印線の下側はそのままで上側だけ拡大してみました。レンズもフィルムも書き込んではいませんが、冒頭の図との対比で予想がつきますでしょうか。この図では四角錐の頂点がレンズ、上側に現れた逆さまの四角錐の底面(逆さまなので上にありますが)がフィルムに該当します。

 

分かりやすくするためもうちょっとだけ拡大して、点に名前も入れて…

 

 

これでどうでしょう！

O,O’はレンズ中心、P,P’はそれぞれのフィルム上で建物の角が写っている点(※2)です。実はこの4点とも座標値が分かるため、めでたく

PからOを通って伸ばした線とP’からO’を通って伸ばした線はP,P’に写っていた建物の角で交わるから直線POと直線P’O’の交点ってことで未知とされてる建物の角の座標値は計算して求められる！今度こそ！！

となります。

 

…

 

ということで、フィルム上で件の建物の角が写っている点P,P’がその建物の角の座標値を求めるときの大もとの起点でした。なんだかものすごく当たり前では？という結論になりましたね。しかも、建物の角の座標値は2直線の交点を求めるだけで計算できそうです。そうすると、あと気になるのは点O,O’,P,P’の座標値って具体的にどうやって求めてるの？という点ですが、続きはまた今度。

 

—

※1 実際、デジタルカメラでは(例えばCCD)イメージセンサが使用されますが、以降便宜的にフィルムと表現します。

※2 第2回も参照。P,P’はデジタルステレオ図化機の利用者がメスマークにより同時に指定します。