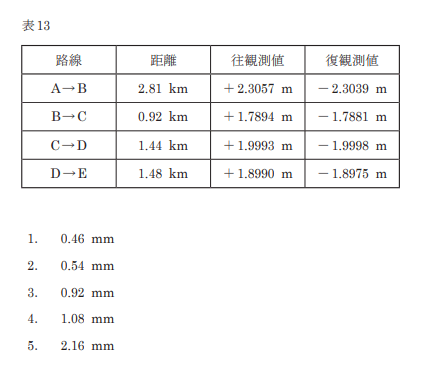
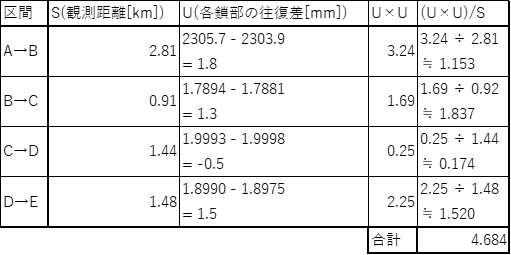
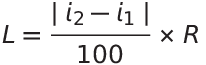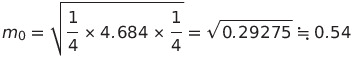測量士試験の過去問題を解くシリーズ、令和2年度試験版の第8回です。
以下、「国土地理院」サイトの 令和2年11月22日の問題を引用して解説して行きます。
〔No.27〕
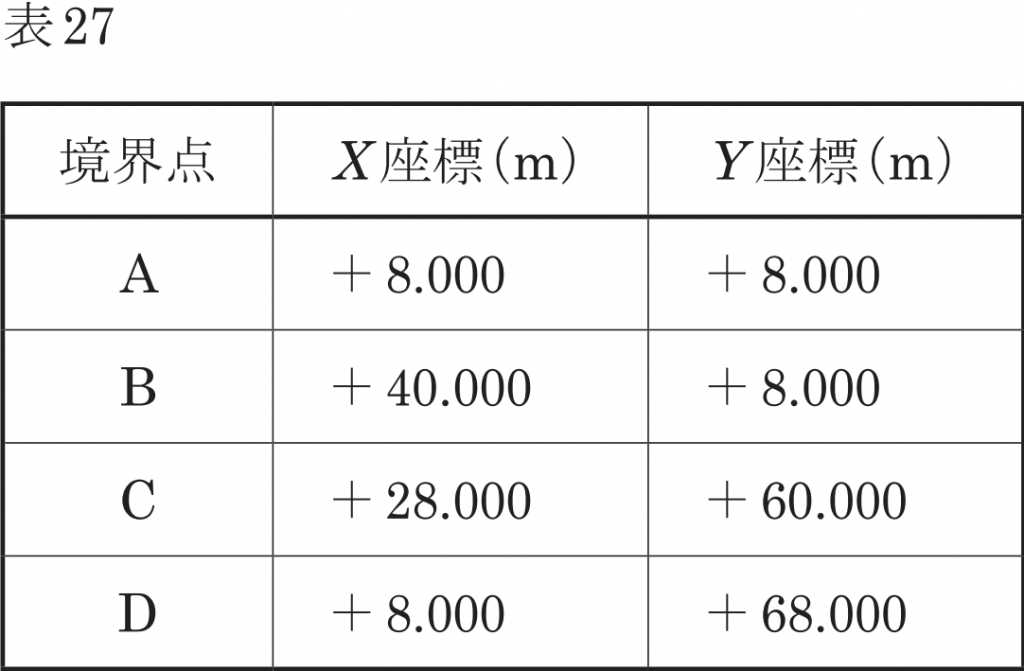
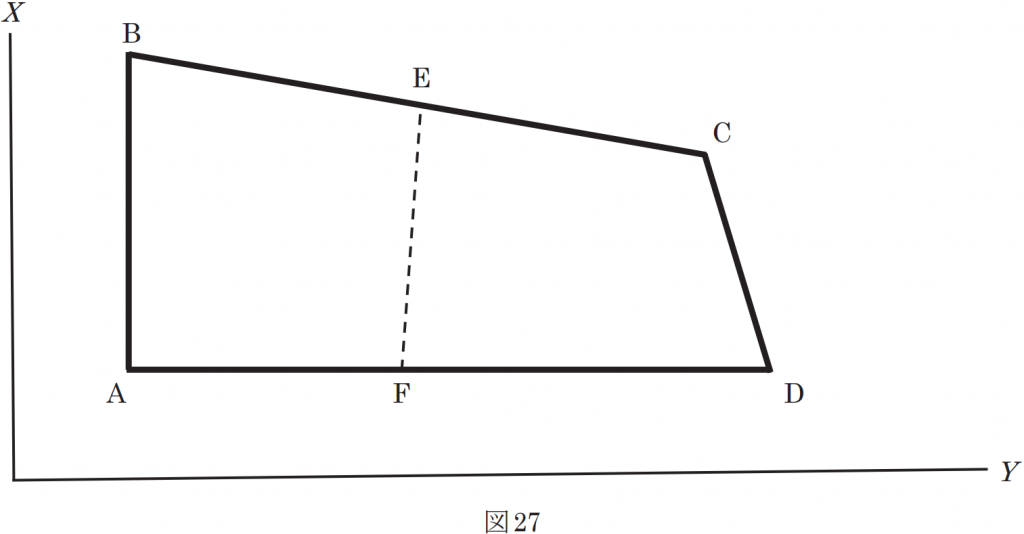
表27は,面積 1,432.000m2の四角形ABCDの土地を構成する各境界点の平面直角座標系(平成14年国土交通省告示第9号)に基づく座標値を示す。公共測量によって,この土地を図27で示すように,面積の等しい四角形ABEF及びFECDの 2つの土地に分割したい。
点EをBE=ECとなる位置に設置したとき,点FのY 座標値は幾らか。最も近いものを次の中から選べ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
1. +27.629m
2. +29.351m
3. +31.077m
4. +33.357m
5. +37.000m
解答は3です。以下、解説です。
まず、点Eの座標を求めます。
問題文よりBE=ECだから、点Bと点Cの中間地点に点Eがあります。
なので点Eの座標は
X=40-(40-28/2)=34
Y=60-(60-8/2)=34
点E(X,Y)=(+34.000,+34.000)
求められた点Eを含む四角形ABEFとFECDは面積が等しいため、四角形ABCDを二等分したものと考えられます。そのため四角形ABEFとFECDそれぞれの面積は四角形ABCDの面積(1,432.000m2)の半分なので
ABEF=FECD=1432.000÷2=716.000 m2
点Fの座標を求めていきます。点FのX座標は点A,Dを結ぶ直線状にあるので点A,DのX座標を見ると2点ともX=+8.000mだから点FのX座標も+8.000となります。
ここで点FのY座標をyとして四角形ABEFの求積表を作っていきますが、ここで点Aを座標原点として仮に置きこの時の点FのY座標をy’(y’=y-8.000)として考えることで計算を楽にして求積表を改めて作ります。
| X | Y | Yn+1-Y n-1 | X(Yn+1-Y n-1) | |
| A | 0 | 0 | -y’ | 0 |
| B | 32 | 0 | 26 | 832 |
| E | 26 | 26 | y’ | 26y’ |
| F | 0 | y’ | -26 | 0 |
| 倍面積 | 1432 | |||
| 面積 | 716 |
求積表から
1432=832+26y’
600=26y’
y’=23.0769⋯≒23.077
y=y’+8.000=23.077+8.000=31.077m
よって、点FのY座標は31.077mとなります。