測量士試験の過去問題を解くシリーズ、令和元年度試験版の第9回です。
以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。
〔No.25〕
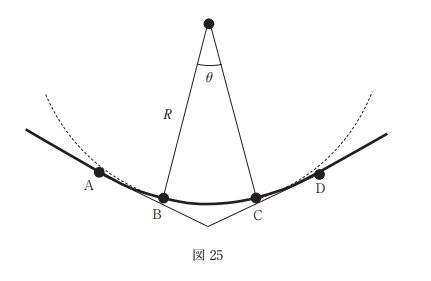
図 25 に模式的に示すように,基本型クロソイド(対称型)の道路建設を計画した。点A及び点Dを クロソイド曲線始点,点B及び点Cをクロソイド曲線終点とし,クロソイドパラメータは 150 m,円曲線の曲線半径 R=250 m,円曲線の中心角θ=30°,円周率π=3.142 とするとき,点Aから点Dの路線長は幾らか。最も近いものを次の中から選べ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
- 221 m
- 266 m
- 311 m
- 336 m
- 361 m
解答は3です。以下解説します。
方針としまして、AB間、BC間、CD間の距離を分割して求めた距離を使用してAからDの路線長を求めます。
AB間とCD間の距離は、クロソイド曲線で表されます。
L=クロソイド曲線の長さ,
R=円曲線の曲線半径,
A=クロソイドパラメータ
と置くと、クロソイド曲線の公式から、
L×R=A^2 …①
が成り立ちます。
クロソイド曲線のAB間またはCD間の距離は等しいのでどちらもLと置けます。
問題文より、
R=250m,
A=150m
と与えられていますので、
AB間またはCD間の距離
=L
=(A^2)÷R …①より
=(150×150)÷250
=90m …②
となります。
BC間の距離は、 円曲線として表されます。
θ=円曲線の中心角,
π=円周率,
R=円曲線の曲線半径
と置くと、
円曲線の距離=2×Π×(θ÷360)×R …③
が成り立ちます。
問題文より、
Π=3.142,
θ=30°,
R=250m
と与えられていますので、
BC間の距離
= 2×Π×(θ÷360)×R …③より
= 2×3.142×(30÷360) ×250
≒130.92 …④
となります。
上記②と④の結果から、
AD間の路線長=AB間の距離+BC間の距離+CD間の距離
≒90+130.92+90
≒310.92 …⑤
となります。
⑤ と問題文の選択枝の中で最も近い値は3番の311mとなります。
以上です。

