測量士試験の過去問題を解くシリーズ、令和元年度試験版の第4回です。
以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。
[R 1-午前No.8 問題] (以下引用開始)
〔No.8〕
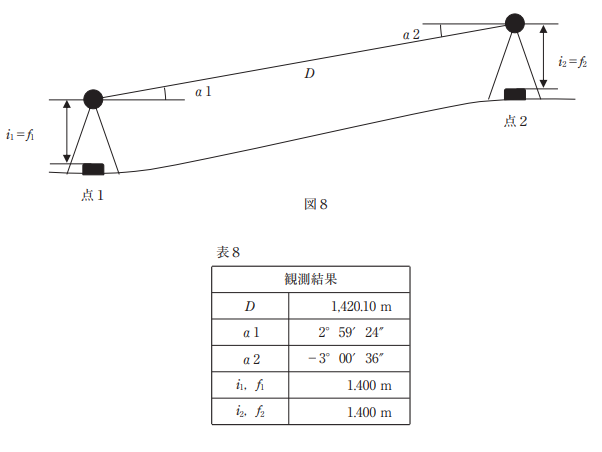
公共測量におけるトータルステーションを用いた1級基準点測量において,図8に示すように標高23.50 m の点1と標高 97.70 m の点2の間の距離及び高低角の観測を行い,表8の観測結果を得た。Dを測定距離,α1 を点1から点2方向の高低角,α2 を点2から点1方向の高低角,i1,f1 を点1の器械高,目標高,i2,f2 を点2の器械高,目標高とするとき,点1,点2間の基準面上の距離は幾らか。最も近いものを次の中から選べ。
ただし,地球の平均曲率半径は 6,370 km,点1,点2のジオイド高を平均した値は 40.00 m を用いるものとする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
1. 1,418.09 m
2. 1,418.11 m
3. 1,418.13 m
4. 1,418.15 m
5. 1,418.17 m
(引用終了)
正解は3です。
基準面上の距離を求めるために、国土交通省サイトの測量機器検定基準の計算式集 付録6のP160-161にある式を引用します。
(以下引用開始)


(引用終了)
問8の文中で与えられた値を式に当てはめて行きます。
D=1420.10m
H1=23.50m+1.400m=24.90m
H2=97.70m+1.400m=99.10m
α1=2°59′24″
α2=-3°00′36″
R=6370km=6370000m
Ne=40.00m
から、
S = 1420.10 × cos(6/2) × 6370000 ÷ ( 6370000 + (24.90 + 99.10) / 2 + 40.00 )
= 1420.10 × 0.99863 × 6370000 ÷ ( 6370000 + 102.00 )
= 1420.10 × 0.99863 × 0.99998
= 1418.1545 × 0.999983
≒ 1418.13
※ cos(3°)= 0.99863 (巻末の関数表 より)
計算式を記憶していないと解きにくい問題だと思います。
以上です。

