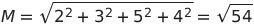測量士試験の過去問題を解くシリーズ、令和2年度試験版の第5回です。
以下、「国土地理院」サイトの 令和2年11月22日の問題を引用して解説していきます。
〔No.15〕
トータルステーションを用いて細部測量を実施した。既知点Aから求める点Bを観測し,方位角T=25°,距離S=190mを得た。この測量において,距離測定の標準偏差が5.95 mm,角度測定の標準偏差が5″であるとしたとき,求める点Bの位置の標準偏差は幾らか。最も近いものを次の中から選べ。ただし,角度1ラジアンは,(2 ×105 )″とする。なお,関数の値が必要な場合は,巻末の関数表を使用すること。
1. 4.8 mm
2. 6.0 mm
3. 6.2 mm
4. 7.0 mm
5. 7.6 mm
解答は5です。以下、解説です。
問題文より角度と距離について標準偏差を考慮して表記すると、方位角はT=25°±5″、距離はS=190m±5.95mmとなります。求めるのは位置の標準偏差なので角度と距離、2つの標準偏差を長さの単位に揃えます。
まず、角度の測定による標準偏差を求めます。はじめに角度測定の標準偏差の表記を度数法からメートル法への変換を行います。ここで、ラジアンについての情報が問題文中で与えられているのでこれを用いて変換します。角度の標準偏差5″をラジアンへ変換します。問題文より1ラジアンは(2 ×105 )″だから
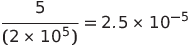
となります。
ここで水平位置の標準偏差を求めます。方位角の標準偏差は解説図-1の様に表すことができます。
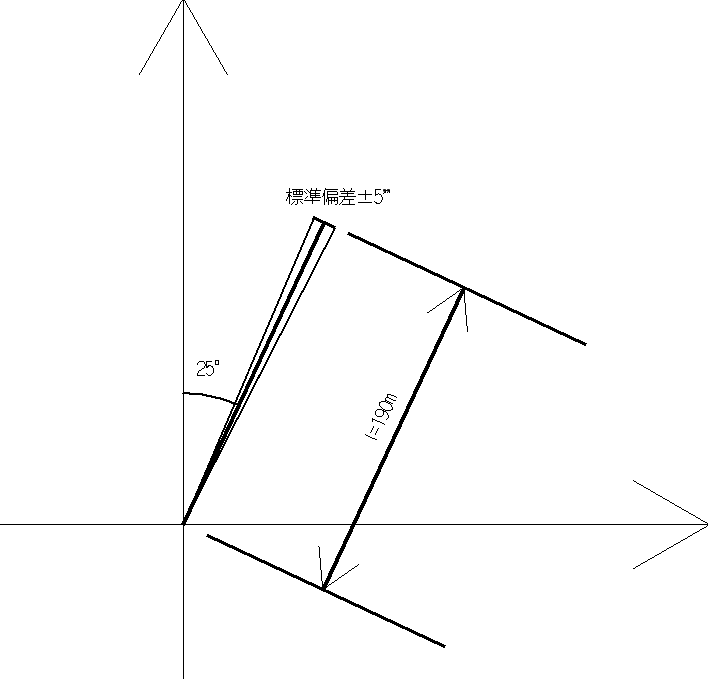
ここから、ラジアンの定義を用います。
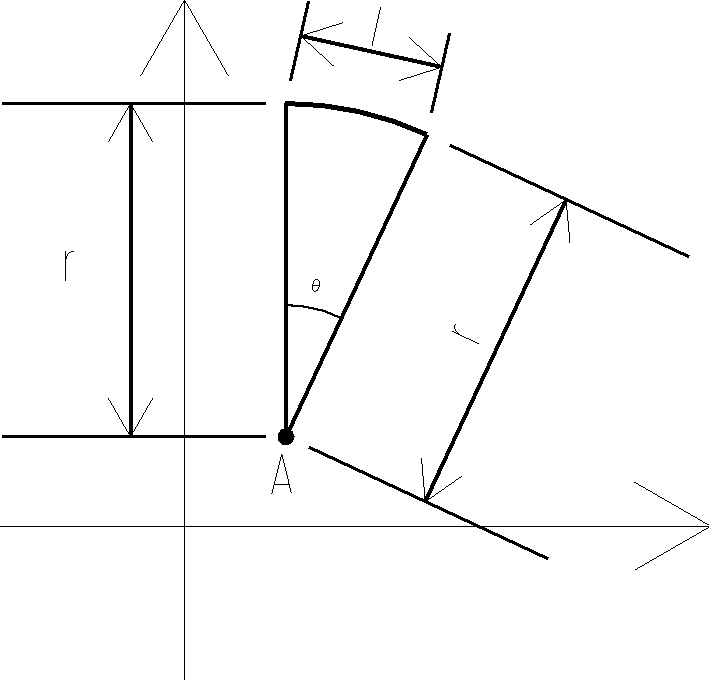
解説図-2より中心角がθで半径がrの扇形の弧の長さlの円弧として考えます。この定義は式1-1で表すことができます。
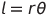
角度による標準偏差を弧の長さlとして、半径rを距離190000mm(190m)、θを求めたラジアン2.5×10-5radとします。これを代入すると
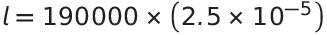
であり、角度による水平位置の標準偏差は4.75mmとなります。
距離の標準偏差はメートル法で単位を揃えられているため、5.95mmをそのまま距離による標準偏差とします。
距離と角度のそれぞれの水平位置に関する標準偏差が求められました。これより位置の標準偏差を求ます。
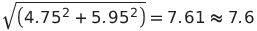
となり、点Bの位置の標準偏差7.6mmが得られます。
解説は以上です。