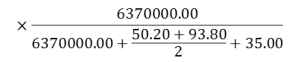測量士試験の過去問題を解くシリーズ第1回です。
今回は平成27年度の午前No6の問題を解いてみます。
[H27-No.6 問題] 公共測量におけるトータルステーションを用いた1級基準点測量において、図6に示すように標高48.80mの点1と標高92.40mの点2との間の距離および高低角の観測を行い、表6の観測結果を得た。 Dを斜距離、α1を点1から点2方向の高低角、α2を点2から点1方向の高低角、i1、f1を点1の器械高及び目標高、i2、f2を点2の器械高及び目標高とするとき、点1、2間の基準面上の距離は幾らか。最も近いものを次の中から選べ。 ただし、地球の平均曲率半径は6,370km、点1、2のジオイド高を平均した値は35.00mを用いるものとする。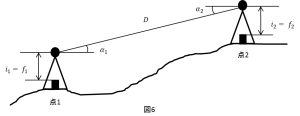
表6 1. 1,246.46m 2. 1,246.48m 3. 1,246.50m 4. 1,246.52m 5. 1,246.54m
この問題は基準面上の距離を求める問題で投影計算の式を覚えていないとどうしようもない問題です。
過去には平成23年度(No8)に与えられる数値が違うだけで同じ問題が出題されています。
投影計算の式は

ここで点1の標高H1は文中に与えられた標高48.80mと表6で与えられているi1,f1(点1の器械高及び目標高) 1.40mの和であるので、
H1=48.80+1.40=50.20m
点2の標高も同様にして
H2=92.40+1.40=93.80m
文中で与えられた数値を式に代入して
より正解は4.となり ます。