測量士試験の過去問題を解くシリーズ、令和元年度試験版の第10回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

 〔No．27〕 　　
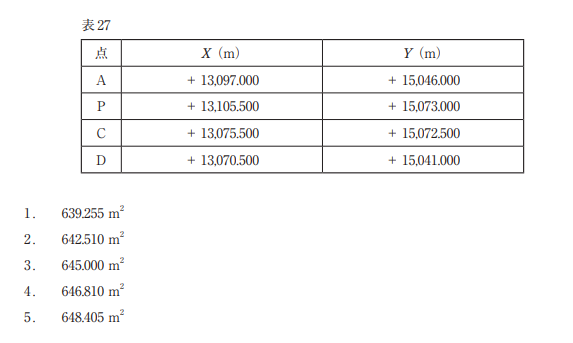
　境界点Ａ，Ｂ，Ｃ，Ｄで囲まれた四角形の土地の面積を求めたい。点Ｂは直接観測できないため，補 助基準点Ｐを設置し，点Ａ，Ｐ，Ｃ，Ｄをトータルステーションを用いて測量し，表 27 に示す平面直 角座標系（平成 14 年国土交通省告示第９号）における座標値を得た。点Ａ，Ｂ，Ｃ，Ｄで囲まれた四 角形の土地の面積は幾らか。最も近いものを次の中から選べ。
　ただし，補助基準点Ｐから点Ｂまでの距離は 10.000 m，点Ｐにおける点Ｂの方向角は 240°とする。なお，関数の値が必要な場合は，巻末の関数表を使用すること。

正解は5です。下記の３ステップで求めます。

ステップ１　ステップ３で計算しやすいように、Ｄ点を原点とした場合の、Ｄ 点 からＡ,Ｐ,Ｃ点への相対的な座標である Ａ’,Ｐ’,Ｃ’,Ｄ’点 を計算します。

ステップ ２　Ｐ’点からＢ’点を求めます。( Ｂ’点 は、Ｄ点 を原点とした場合の、 Ｄ点からＢ点への相対的な座標です。)

ステップ ３　与えられた4頂点から四角形の面積を求める公式を使用して四角形Ａ’Ｂ’Ｃ’Ｄ’の面積を求めます。

ステップ１
ステップ３で計算しやすいように、Ｄ点を原点とした場合の、Ｄ 点 からＡ,Ｐ,Ｃ点への相対的な座標である Ａ’,Ｐ’,Ｃ’,Ｄ’点 を計算します。

Ａ’＝Ａ － Ｄ
　＝(x1, y1)
　＝(13097.000 – 13070.500, 15046.000 – 15041.000)
＝(26.500, 5.000)
Ｐ’＝Ｐ － Ｄ
　＝(13105.500 – 13070.500, 15073.000 – 15041.000)
　 ＝(35.000, 32.000)
Ｃ’＝Ｃ － Ｄ
　 ＝(x3, y3)
　＝(13075.500 – 13070.500, 15072.500 – 15041.000)
　＝(5.000, 31.500)
Ｄ’＝Ｄ － Ｄ
　＝(x4, y4)
　＝(13070.500 – 13070.500, 15041.000 – 15041.000)
＝(0.000, 0.000)

ステップ２
Ｐ’点からＢ’点を求めます。( Ｂ’点 は、Ｄ点 を原点とした場合の、 Ｄ点からＢ点への相対的な座標です。)

問題文より、点Ｐから 点Ｂまでの距離は 10.000 m，点Ｐにおける点Ｂの方向角は 240° であることから、下記の様に求められます。

Ｂ ＝Ｐ＋ (cos240° ×10.000 , sin240°×10.000)
より、
Ｂ－Ｄ＝Ｐ＋ (cos240° ×10.000 , sin240°×10.000) －Ｄ
Ｂ’＝Ｐ’＋ (cos240° ×10.000, sin240°×10.000)
　＝(x2, y2)
　＝(35.000 – 0.500 × 10.000, 32.000 – 1.732 ÷ 2.000 × 10.000)
　＝(30.000 , 23.340)

ステップ３
与えられた4頂点から四角形の面積を求める公式を使用して四角形Ａ’Ｂ’C’Ｄ’の面積を求めます。

ステップ1とステップ2から、 点 Ａ’Ｂ’ C’Ｄ’ の座標は下記のようになります。
Ａ’＝(x1, y1) ＝(26.500, 5.000)
Ｂ’＝(x2, y2) ＝(30.000 , 23.340)
Ｃ’＝(x3, y3) ＝(5.000, 31.500)
Ｄ’＝(x4, y4) ＝(0.000, 0.000)

Ｓ＝与えられた4頂点から四角形 Ａ’Ｂ’C’Ｄ’ の面積を求める公式より
　＝0.5×(x1y2 – x2y1 + x2y3 – x3y2 + x3y4 – x4y3 + x4y1 – x1y4)
　＝0.5×(x1y2 – x2y1 + x2y3 – x3y2) 　　※ x4とy4は0のため
　＝0.5×(26.500 × 23.340 – 30.000 × 5.000 + 30.000 × 31.500 – 5.000 × 23.340)
　＝0.5×1296.810
　＝648.405

よって解答は5となります。
ある点からの相対的な点を求めたり、与えられた頂点から四角形の面積を求める公式を覚えていないと計算がとても煩雑になります。

以上です。