測量士試験の過去問題を解くシリーズ、令和2年度試験版の第1回です。

以下、「国土地理院」サイトの 令和2年11月22日の問題を引用して解説して行きます。

〔No．4〕 　
図4に示すような三次元直交座標系において，ある点（x，y，z）をZ軸の周りに図4で示す方向にθ回転させたときの点（x’，y’，z’）の座標は，次の式4で表される。

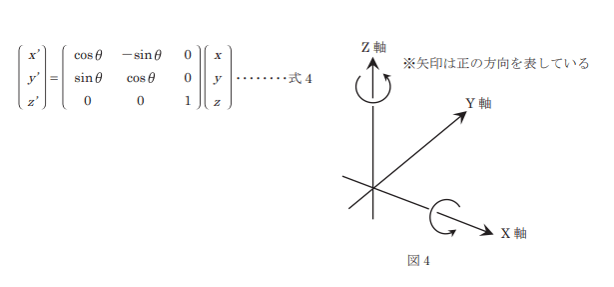
点P（2.000，－1.000，3.000）をZ軸周りに図4で示す方向に60°回転させたとき，移動後の点P’の座標は，式4より，点P’（1.866，1.232，3.000）となる。この点P’（1.866，1.232，3.000）を，さらにX軸の周りに図4で示す方向に30°回転させたとき，移動後の点P”の座標は幾らか。Z軸周りの回転を表す式4を参考に，X軸周りの回転を表す式を立てて計算し，最も近いものの組合せを次の中から選べ。なお，関数の値が必要な場合は，巻末の関数表を使用すること。

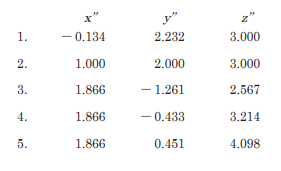
正解は4です。下記の2ステップで求めます。

ステップ1
X軸周りの回転を表す式を求めます。

ステップ2
ステップ1で求めた式を使用して回転後の座標を求めます。

ステップ1
X軸周りの回転を表す式を求めます。 まずは考えやすくするために、図4のX軸を上に向くように回転させます。

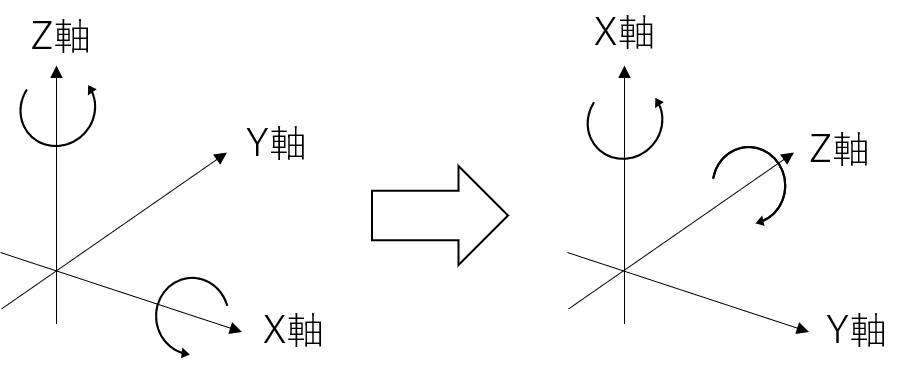
与えられた式4は図を変換させる前のZ軸を反時計回りに回転させた式であり、変換後のX軸を反時計回りに回転させた式は次のように変換できます。

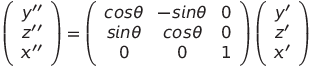
ステップ2
ステップ1で求めた式を使用して回転後の座標を求めます。 点P’（1.866，1.232，3.000）をＸ軸周り30°回転させた点P”を求める式は

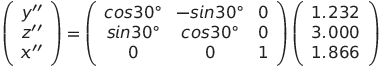
となります。計算すると、

y” = cos30°×　1.232　+  -sin30°×　3.000　+  0 ×　1.866
 ≒　-0.433
z” = sin30°×　1.232　+   cos30°×　3.000　+  0 ×　1.866
 ≒　3.214
x” = 　0　×　1.232　+ 　0　×　3.000　+　1　×　1.866
 ≒　1.866

よって点P’（1.866，1.232，3.000）をＸ軸周り30°回転させた点P”は4の（1.866、-0.433、3.214）になります。