測量士試験の過去問題を解くシリーズ、令和元年度試験版の第7回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

 〔No．14〕
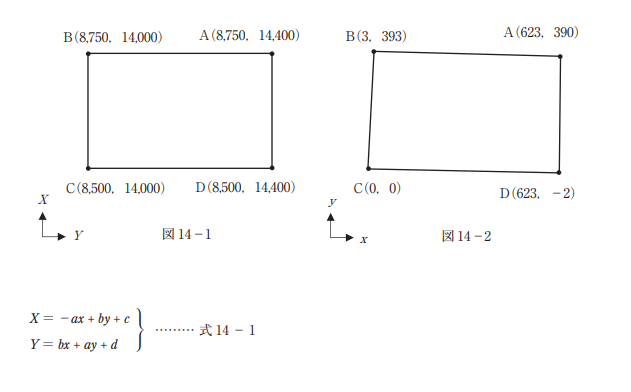
　　　新たに完成した宅地造成地の既成図を数値地形図データの修正に用いることとした。この既成図の図 郭四隅の点Ａ，Ｂ，Ｃ，Ｄには，図 14－1 に示す平面直角座標系（平成 14 年国土交通省告示第 9 号） における座標値が記載されていた。また，これをスキャナにより数値化し，コンピュータソフトウェア を用いてスクリーンモニター上で図郭の四隅の点を計測したところ，図 14－2 に示す座標値を得た。
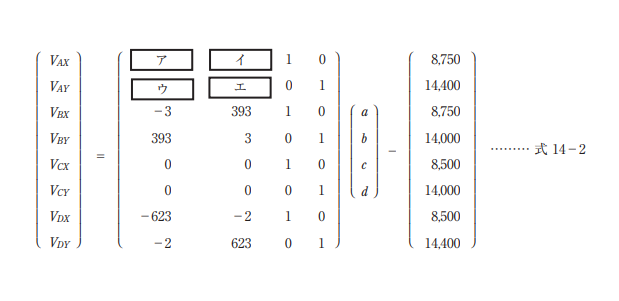
　　　この数値化された既成図を，式 14－1 の変換式を使って補正し，数値地形図データとの位置合わせ を行いたい。変換係数 a，b，c，d を最小二乗法により求めるための観測方程式が次のページの式 14－ 2 である。  ア  ～  エ  に入る数値の組合せとして正しいものはどれか。次のページの中 から選べ。
　　　ただし，変換式の X，Y は既成図の座標値，x，y はスクリーンモニター上で計測した座標値，a，b， c，d は変換係数とし，観測方程式の VAX，VBX，VCX，VDX は点 A，B，C，D 各点の平面直角座標系に おける X 座標の残差を，VAY，VBY，VCY，VDY は Y 座標の残差を示すものとする。

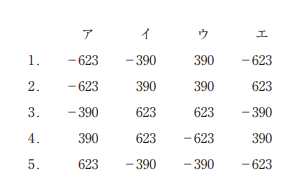
解答は2です。以下解説して行きます。

図14-2の B(3, 393) は 、図2の式14-2から VBXと VBY を求めるための
図1の式14-1における a, b, c, d の値は、a=3, b=393, c=1, d=1
となります。

図14-2の C(0, 0) は 、図2の式14-2 から VCXと VCY を求めるための
図1の式14-1における a, b, c, d の値は、a=0, b=0, c=1, d=1
となります。

図14-2の D(623, -2)は、図2の式14-2 から VDXとVDYを求めるための
図1の式14-1における a, b, c, d の値は、a=623, b=-2, c=1, d=1
となります。

図14-2の A(623, 390)は、図2の式14-2 から VAXとVAYを求めるための
図1の式14-1における a, b, c, d, の値は、B, C, Dと同様に当てはめて、
a=623, b=390, c=1, d=1 となり、上記表1では、
2.の ア=-623, イ=390, ウ=390, エ=623
が該当します。

以上です。