測量士試験の過去問題を解くシリーズ、H30年度試験版の第6回です。
以下、「国土地理院」サイトの平成30年5月20日の問題を引用して解説して行きます。
[H30-午前No.14 問題] トータルステーション(以下「TS」という。)を用いて,放射法により標高を求めたい。既知点Aから求点Bを TS で観測したところ,測定距離 80.000 m,高低角 35° 00′ 00″を得た。使用した TS の距離測定の精度(標準偏差)が 5 mm+5×10-6 D(D は測定距離),角度測定の精度(標準偏差)が 5″の場合,求点Bの標高の計算結果の精度(標準偏差)は幾らか。最も近いものを次の中から選べ。 ただし,TS による距離測定と角度測定は互いに影響を与えないものとし,その他の誤差は無視してよいものとする。また,角度 1 ラジアンは,(2×10^5)″とする。 なお,関数の値が必要な場合は,巻末の関数表を使用すること。 1. 3.1 mm 2. 3.5 mm 3. 4.6 mm 4. 5.4 mm 5. 5.8 mm
正答は、2です。
解答に至るまでには、下記の3つのステップを経ます。
(a) TS の距離測定の精度(標準偏差)から測定距離の標準偏差の高さ要素(α)を求めます。
(b) TS の角度測定の精度(標準偏差)からA-B方向に直行する方向の標準偏差の高さ要素(β)を求めます。
(c) 標準偏差の高さ要素(α)、標準偏差の高さ要素(β)および、距離測定と角度測定は互いに影響を与えない条件から、誤差伝搬の法則を用いて総合的な標準偏差を求めます。
それでは始めます。
(a) TS の距離測定の精度(標準偏差)から測定距離の標準偏差の高さ要素(α)を求めます。
(1) 問題から与えられた条件は下記の通りです。
\[
\begin{align*}
測定距離 & = 80.000 m \\
使用した TS の距離測定の精度(標準偏差)& = 5 mm + 5 \times 10^{-6} \times D(D は測定距離)\\
\end{align*}
\]
(2) 測定距離の標準偏差を求めます。
\[
\begin{align*}
測定距離の標準偏差 & = 5mm + 5 \times 10^{-6} \times 80.000m \\
& = 5mm + 0.4mm \\
& = 5.4mm…(2)の結果
\end{align*}
\]
(3) 測定距離の標準偏差の高さ要素(α)を求めます。
測定距離の標準偏差の高さ要素(α)を求めるために下図の関係を用いています。
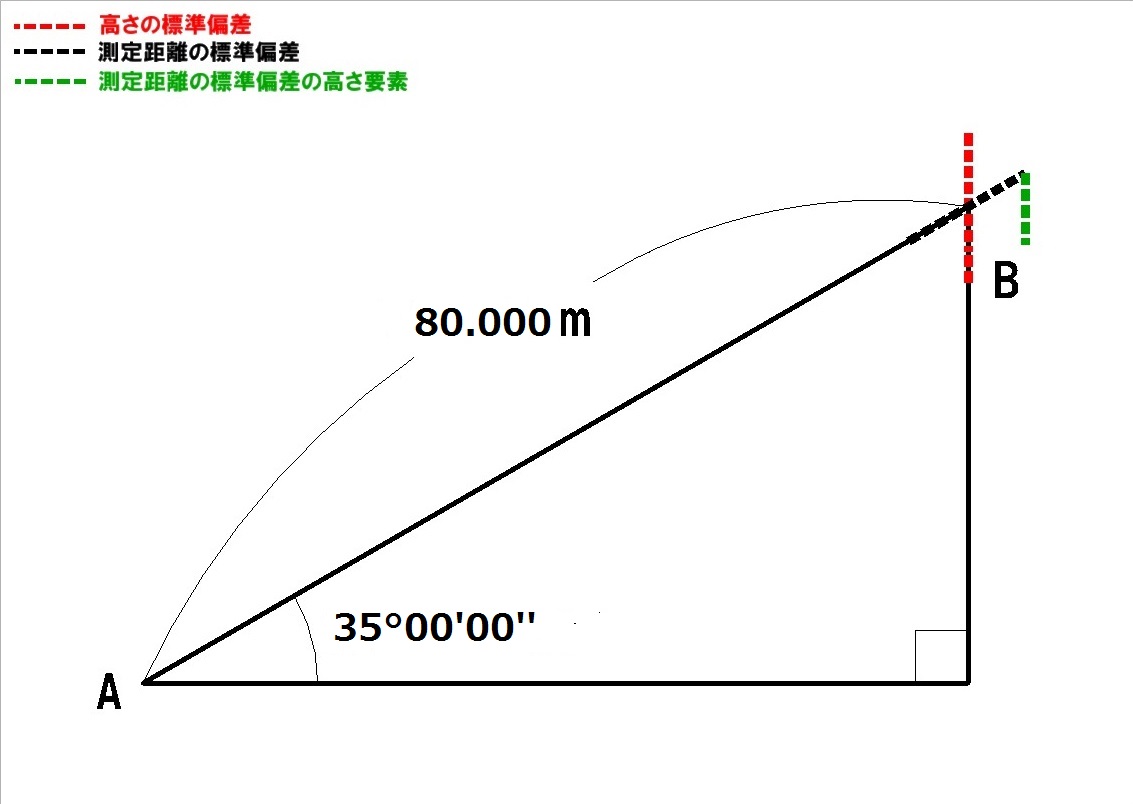
[図1 測定距離の標準偏差と、測定距離の標準偏差の高さ要素(α)の関係図]
\[
\begin{align*}
測定距離の標準偏差 & = 5.4mm…(2)の結果より\\
sin(35度) &= 0.57358 (巻末より) \\
測定距離の標準偏差の高さ要素(α) &= 測定距離の標準偏差 \times sin(35度) \\
&= 5.4 \times 0.57358 \\
&\risingdotseq 3.0973…(3)の結果
\end{align*}
\]
(b) TS の角度測定の精度(標準偏差)からA-B方向に直行する方向の標準偏差の高さ要素(β)を求めます。
(4) 問題から与えられた条件は下記の通りです。
\[
\begin{align*}
測定距離 & = 80.000 m \\
使用した TS の角度測定の精度(標準偏差)& = 5″ \\
1 ラジアン &= (2 \times 10^5)″
\end{align*}
\]
(5) 角度測定の精度は微小値のため、A-B方向に直行する方向の距離は、既知点Aから求点Bまでの測定距離を等辺とする2等辺三角形の底辺の長さに比例するとみなせます。下記の式で底辺の長さを求めます。
\[
\begin{align*}
2等辺三角形の底辺 & = 2等辺三角形等辺 \times \frac{角度測定の精度}{1 ラジアン}…(5) \\
\end{align*}
\]
(6) A-B方向に直行する方向の標準偏差を求めます。
\[
\begin{align*}
2等辺三角形の底辺 & = 2等辺三角形等辺 \times \frac{角度測定の精度}{1 ラジアン}…(5)より \\
& = 80.000m \times \frac{5″}{(2 \times 10^5)″} \\
& = 0.002m \\
& = 2mm…(6)の結果
\end{align*}
\]
(7) A-B方向に直行する方向の標準偏差の高さ要素(β)を求めます。
A-B方向と直行する方向の標準偏差の高さ要素(β)を求めるために下図の関係を用いています。
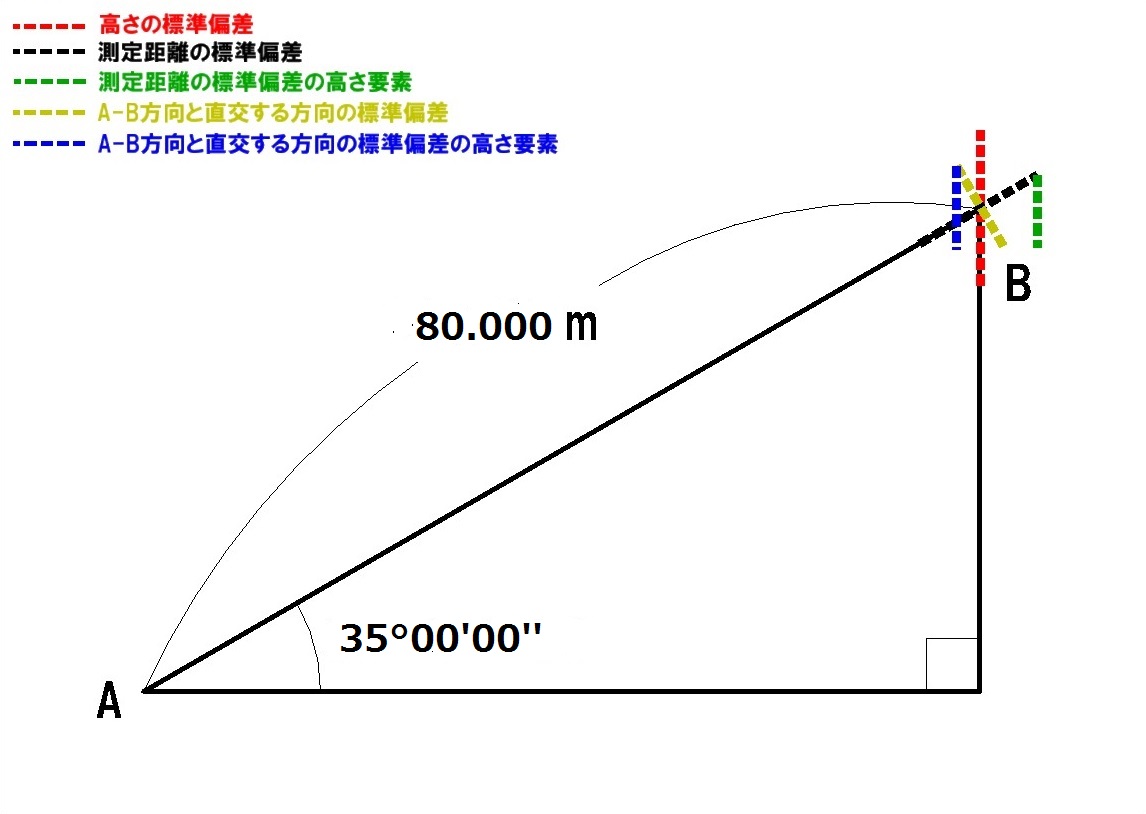
[図2 A-B方向と直行する方向の標準偏差とA-B方向と直行する方向の標準偏差の高さ要素の関係図]
\[
\begin{align*}
cos(35度) &= 0.81915 (巻末より) \\
A-B方向に直行する方向の標準偏差の高さ要素(β) &= A-B方向に直行する方向の標準偏差 \times cos(35度) \\
&= 2mm \times 0.81915 \\
&\risingdotseq 1.6383…(7)の結果
\end{align*}
\]
(c) 標準偏差の高さ要素(α)、標準偏差の高さ要素(β)および、距離測定と角度測定は互いに影響を与えないという条件から、誤差伝搬の法則を用いて総合的な標準偏差を求めます。
\[
\begin{align*}
標準偏差の高さ要素(α) & \risingdotseq 3.0973 \\
標準偏差の高さ要素(β) & \risingdotseq 1.6383 \\
誤差伝搬の法則式 & = \sqrt{ 標準偏差の高さ要素(α)^2 + 標準偏差の高さ要素(β)^2 } \\
& \risingdotseq \sqrt{ 3.0973^2 + 1.6383^2 } \\
& \risingdotseq \sqrt{ 9.5932 + 2.6840 } \\
& \risingdotseq 3.503
\end{align*}
\]
よって解答は、正答は、2(3.5mm)となります。
No.14の解説は以上です。

