測量士試験の問題を解くシリーズ第9回です。
今回は平成27年度の午前No.12とNo.26を解きます。
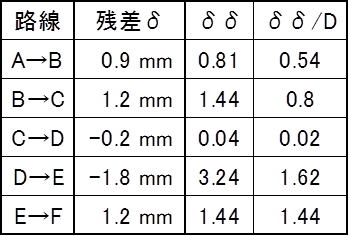
平成27年度 測量士試験 午前 No.12 水準点AからFまで水準測量を行い、表12の結果を得た。1km当たりの観測の標準偏差の値は幾らか。最も近いものを次の中から選べ。 表121. 0.47 mm 2. 0.52 mm 3. 0.66 mm 4. 0.83 mm 5. 0.94 mm
路線ごとの残差δ、残差の2乗δδ、残差の2乗を距離Dで割ったδδ/Dを求めると、
これより、標準偏差σは、路線数n=5より
以上より、答えは1となります。
次に平成27年度 測量士試験 午前 No.26を解きます。
平成27年度 測量士試験 午前 No.26 図26に示すように、渋滞緩和を目的として、現在使用している道路ABC(以下「現道路」という。)を改良し、新しい道路AC(以下「新道路」という。)の建設を計画している。新道路は基本型クロソイド(対称型)からなり、主接線は現道路の中心線と一致するものである。このとき、新道路の路線長は、現道路の路線長と比べ何m短縮されるか。最も近いものを次の中から選べ。 ただし、円曲線半径R=220m、交角I=86°、クロソイドパラメータA=120m、円曲線部分の中心角α=69°、円周率π=3.142とする。また、主接線をX軸とし、その原点をクロソイド曲線の始点としたとき、円曲線部分の中心のX座標=32.7m、移程量ΔR=0.8mとする。
図26 1. 16 m 2. 81 m 3. 111 m 4. 147 m 5. 396 m
以上より、現道路と新道路の路線長の差を求めると、
以上より、答えは2となります。

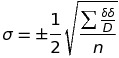

コメント失礼いたします。
路線長LBの解238.4423mが計算通りにならないのですが
計算手順をご教授いただけないでしょうか。
初歩的な質問で申し訳ありませんが、よろしくお願いいたします。
コメントありがとうございます。
混乱させてしまい申し訳ございません、
計算過程が無いのでおかしい点が分かりにくいですね。
上の計算ですが、正確には円周率を3.142で計算すべきところ3.14で概算しています。
問題文中の3.142を使ったり、試験時に配布される関数表
(tan43°の値がπを使わず直接参照できるかと思います)を使ったりすると、
正答となる選択肢は同じですが数十センチほど数値が大きくなるはずです。
また不明な点等ございましたら、お気軽にコメント下さい。