測量士試験の過去問題を解くシリーズ第7回です。
今回は平成27年度測量士試験・午前のNo11について解説します。
図11に示す路線において、既知点A、Dから新点B、Cの標高を求めるために公共測量における水準測量を実施した。 表11の結果が得られたとき、各路線の観測方程式は式11-1で、正規方程式は式11-2で表される。 [ア]~[オ]に入る数値の組合せとして最も適当なものはどれか。 次から選べ。 ア イ ウ エ オ 1. 35.2664 -30.2108 2 75.6332 10.0050 2. 35.2664 -30.2108 0.25 13.9170 10.0050 3. 35.2664 -30.2108 0.25 3.7162 20.2058 4. 24.7336 -29.7892 0.25 11.2838 9.7942 5. 24.7336 -29.7892 2 65.4324 20.2058 ただし、既知点A及びDの標高は30.0000mとする。 また、式中のV1、V2、V3は路線(1)、(2)、(3)の観測高低差の残差、X1、X2は新点B、Cの標高の最確値である。 なお、図11の矢印は観測方向を表す。
図11
| 路線 | 距離 | 観測高低差 | 1kmあたりの観測の標準偏差 |
| (1) | 4.0 km | +5.2664 m | 0.5 mm |
| (2) | 1.0 km | -5.1004 m | 1.0 mm |
| (3) | 2.0 km | -0.2108 m | 2.0 mm |
表11
まずは[ア]、[イ]を求めるために各路線の観測方程式を作業規程の準則(付録6 計算式集) (平成25年3月29日一部改正) の水準測量の3.1.1 観測方程式に記載の次式を用いて作ります。
各路線の観測方程式は次のようになります。
これより、[ア]は35.2664、[イ]は-30.2108となります。
次に[ウ]を求めます。
重量行列Pの対角要素は作業規程の準則第70条第1項第一号より
「距離の逆数を重量とする」とあるので路線(1)の距離4.0kmの
逆数0.25となります。
[エ]、[オ]を求めるために正規方程式A’PAX=A’PLを計算します。
定数部分を取り出してLは
重量行列Pは
まず、A’Pを計算します。
A’はAの転置行列であるので
最後にA’PLを計算して
以上より[エ]13.917、[オ]10.005となり2が正解となります。

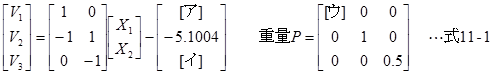
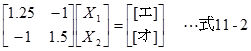
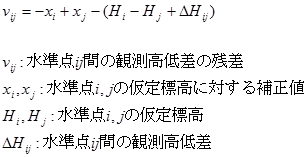
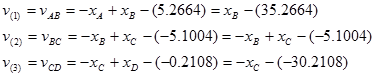
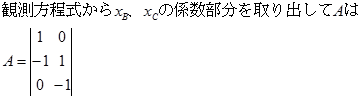
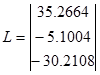
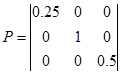
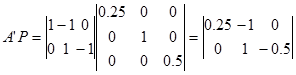
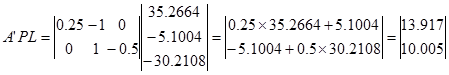
いつも大変お世話になっております。
新点B,Cの仮定標高はそれぞれどう求められるかご教授願願えますでしょうか。
よろしくお願いします。
観測方程式を変形して
vij = -xi + xj – (Hi – Hj + ΔHij)
= -(xi + Hi) + (xj + Hj) – ΔHij
としたときの(xi + Hi)、(xj + Hj)をxAやxBに
置き換えて式を立てているので
この問題では仮定標高を求める意味は特にありません。