測量士試験の過去問題を解くシリーズ、H30年度試験版の第8回です。

以下、「国土地理院」サイトの平成30年5月20日の問題を引用して解説して行きます。

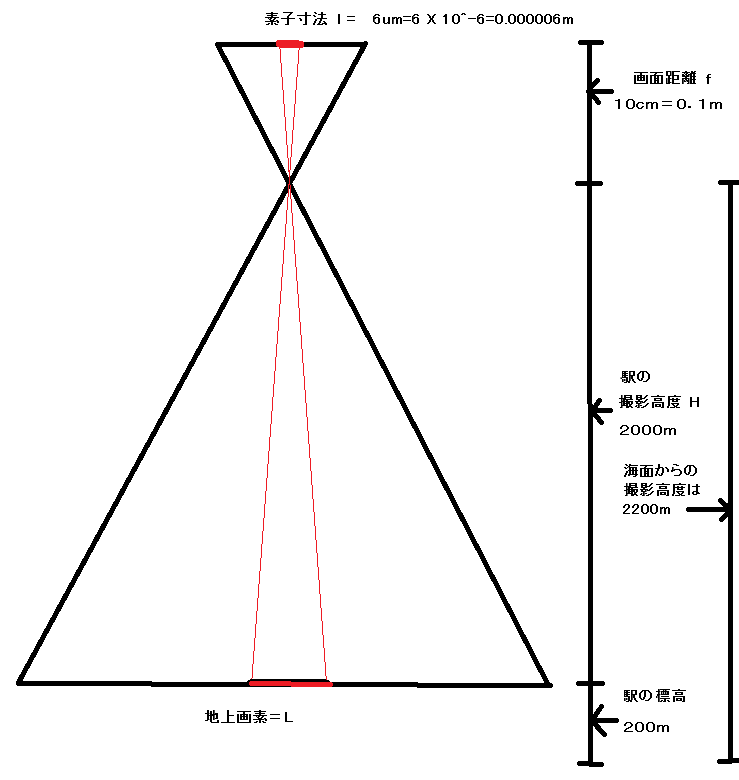
[H30-午前No.19 問題]

 〔No．19〕
　　画面距離 10 cm，画面の大きさ 12,000 画素×8,000 画素，撮像面での素子寸法 6 μm のデジタル航空カメラを用いて，海面からの撮影高度 2,200 m で鉛直空中写真撮影を行った。この写真に写っている駅の長さを数値写真上で計測すると 1,000 画素であった。この駅を縮尺 1 /2,500 の地図にプロットしたとき，地図上での長さは幾らか。最も近いものを次の中から選べ。
　　ただし，この駅は写真の短辺に平行に写っており，標高 200 m の地点に水平に設けられているものとする。
　　なお，関数の値が必要な場合は，巻末の関数表を使用すること。

　　1. 43 mm
　　2. 48 mm
　　3. 53 mm
　　4. 58 mm
　　5. 63 mm

正答は、2です。

問題文を図示して整理します。

まず、駅の標高における地上での画素の長さ Lを求めます。

\[
\begin{align*}
\frac{l}{L}& = \frac{f}{H}
\end{align*}
\]

の関係から、

\[
\begin{align*}
L \times 0.1 & = 0.000006 \times 2000
\end{align*}
\]

となり、

\[
\begin{align*}
駅の標高における地上での画素の長さ L & = 0.12m
\end{align*}
\]

が求まります。

問題文から、駅の長さを数値写真上で計測すると 1000画素なので、

\[
\begin{align*}
駅の長さ & = L \times 1000(画素) \\
& = 120m
\end{align*}
\]

となります。

駅の長さを、縮尺 1 /2,500の地図にプロットすると、

\[
\begin{align*}
駅の長さを、縮尺 1 /2,500の地図にプロット　& = \frac{120m}{2500}　\\
& = 0.048m \\
& = 48mm
\end{align*}
\]

となります。

以上です。

[暁の津門大箇町、冬至間近]