測量士試験の過去問題を解くシリーズ、H29年度試験版の第8回です。

今回はH29年度午前No.15の問題を解いていきます。

[H29-午前No.15 問題]
トータルステーション（以下「TS」という。）を用いて，放射法により標高を求めたい。
既知点Aから求点B をTS で観測したところ，測定距離120.000 m，高低角30°00′00″を得た。
使用したTS の距離測定の精度（標準偏差）が5 mm＋5×10－6D （D は測定距離），
角度測定の精度（標準偏差）が5″の場合，求点B の標高の計算結果の精度（標準偏差）は幾らか。
最も近いものを次の中から選べ。

ただし，TS による距離測定と角度測定は互いに影響を与えないものとし，
その他の誤差は無視してよいものとする。
また，角度1 ラジアンは，（2×105）″とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。

1． 3.8 mm
2． 5.1 mm
3． 5.6 mm
4． 10.5 mm
5． 16.8 mm

正答は1です。

解説していきます。

この問題は、距離測定と角度測定の標準偏差から、標高の標準偏差を求める問題です。

まず、問題文より、距離測定による誤差の範囲は

また、角度測定による誤差の範囲は

となります。
これらは、前者が距離測定方向(AB方向)の誤差の範囲、後者が距離測定方向と直交する方向の誤差の範囲に該当するので、それぞれ標高方向の要素を取り出します。（下図参考）

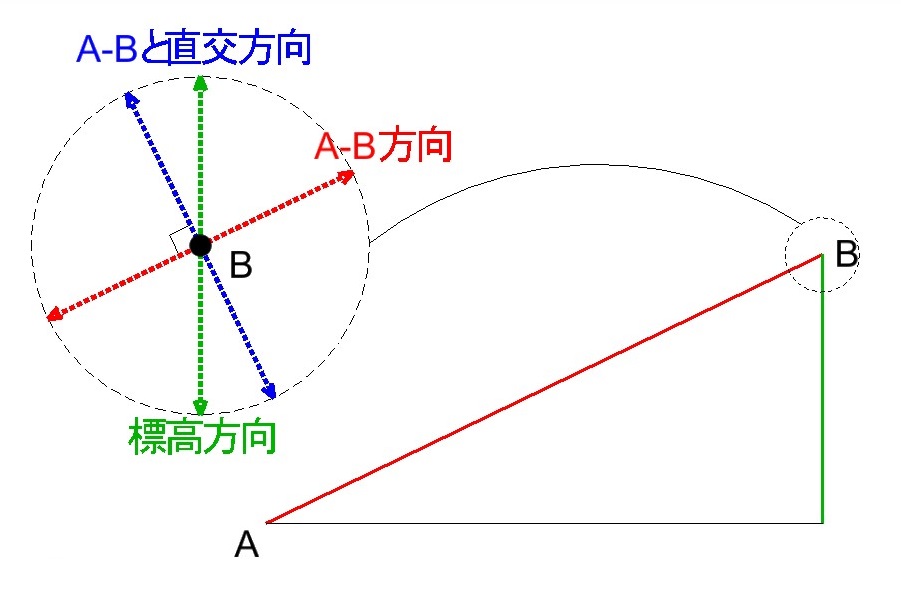
まず、高低角30°00′00″より、距離測定による誤差の範囲の標高方向の要素は

また、距離測定方向と直交する方向の誤差の範囲の標高方向の要素は

となります。(巻末の関数表使用)

これらの値及び誤差伝搬の法則から

巻末の関数表より、

とおくことができ、この範囲におさまるのは解答番号1の3.8mmのみなので答えは1と解けます。

こちらの問題は基本的には図をイメージして、必要な形に変換していくのが解きやすいです。
また、今回の問題は昨年試験のNo.13の値が変わっているだけの問題です。解き方は同じですが、解説の流れや図の描き方は少々異なるので、参考程度にご覧になってください。
計算自体は難しくないので、ぜひ解き方を覚えてください。

No.15の解説は以上です。