測量士試験の過去問題を解くシリーズ、H29年度試験版の第5回です。

今回はH29年度午前No.5、8の2問を解いていきます。
No.5から解説します。

次の式は，平面上の点（x，y）を原点（0，0）を中心にΘ回転させた場合の点（X，Y）の座標
を表す式を行列表記したものである。x = 2.0，y = －1.0，Θ = 150°とした場合，X，Y の組合
せとして最も適当なものはどれか。次の中から選べ。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。




       X        Y
1． -0.914    1.707
2． -1.232    1.866
3． -2.232    0.134
4． -2.732    0.366
5． 2.232     0.134

正答は2です。

計算しながら解説していきます。
まず、問題文に記載されているx = 2.0，y = －1.0，Θ = 150°を代入します。
今回、sin、cosの値は、

sin(Θ+90°)=cosΘ
cos(Θ+90°)=-sinΘ

の公式と巻末の関数表から求めたものを使います。それぞれの値を代入すると、

この行列式の式の右辺を解くと、

となり、

とおけるため、最も近い値をしめしているのは2と解けます。

この問題は三角関数と行列の基本的なルールで解けるため、わからなかった方はそちらの復習をしてください。
特に三角関数は使うことが多いので重要です。

続いて、No.8を解説します。

基準点A，B 間の距離を測定しようとしたところ，障害物があったため，図8 に示すように，
それぞれ偏心点A2，B2に偏心して観測を行った。観測により得られた値は，表8 のとおりであ
る。基準点A，B 間の基準面上の距離S は幾らか。最も近いものを次の中から選べ。
ただし，α1，α2は偏心角，e1，e2は偏心距離，S1は偏心点A2，B2 間の距離である。また，
距離はすべて基準面上の距離に補正されているものとする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。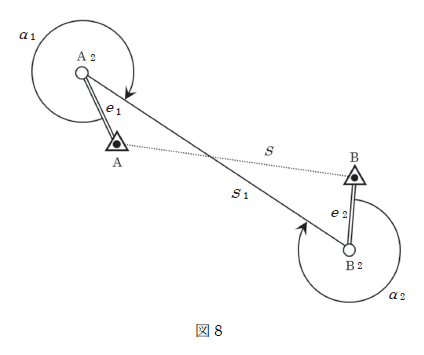



1． 1,936.699m
2． 1,937.617m
3． 1,988.557m
4． 1,995.946m
5． 1,998.975m

正答は2です。

解説していきます。

まず、線SとS₁の交点をPとして、2線のなす角の角度をΘとおきます。
また、点A₂とPからなる線を線S_A、点B₂とPからなる線を線S_Bとおきます。

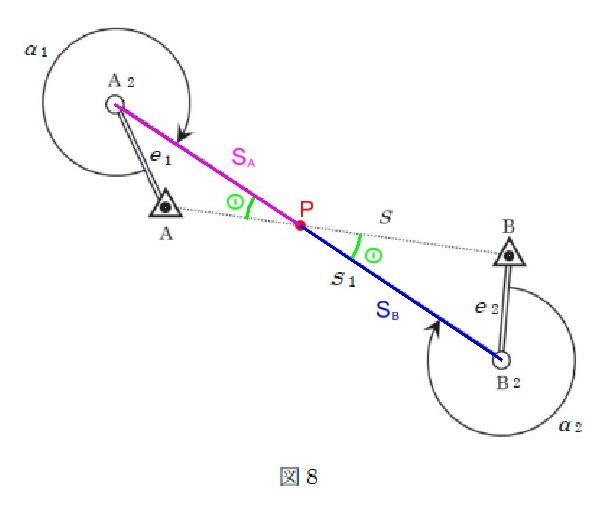
これより、
・・・➀

また、正弦定理より、
・・・➁
・・・➂

とおけます。
この➀、➁、➂を整理します。
➁を整理すると、

同様に➂を整理すると、

上2つの式を➀に代入すると、

となります。これをsinΘについて解いていきます。
加法定理より、

巻末の関数表から、角度のわかっているsin、cosを代入すると、

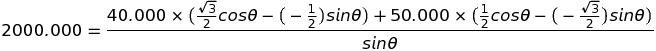
√3は巻末の関数表の値を代入して、整理します。

問題文から、Θはごく小さな正の角度であると判断でき、これは第1象限に含まれるので、

また、
・・・➃

かつ、正弦定理より、
・・・➄

・・・➅

➄、➅に求めたsinΘを代入して整理すると、

となり、答えは最も値の近い2となります。

また、作業規程の準則(国土地理院ウェブサイト)の付録6　計算式集内の基準点測量の2.2.3　に記載されている式を覚えていれば、多少の計算で解答できます。

今回のNo.8は公式を用いる方が実用的かもしれませんが、本番で公式を思い出せない場合はその場で解法を導く必要があるので、過去問で色々な解法を探してみるのもよいのではないでしょうか。

今回の記事は以上です。