測量士試験の過去問題を解くシリーズ、H29年度試験版の第12回です。
今回はH29年度午前No.27の問題を解いていきます。
[H29-午前No.27 問題] 図27 は，境界点A，B，C を順に直線で結ぶ境界線ABC で区割りされた甲及び乙の土地を表したものであり，表27 は，トータルステーションを用いて現地で角度及び距離を測定した結果である。 甲及び乙それぞれの土地の面積を変えずに，境界線AP で区割りして土地を整正するためにはCP間の距離を幾らにすればよいか。最も近いものを次の中から選べ。 なお，関数の値が必要な場合は，巻末の関数表を使用すること。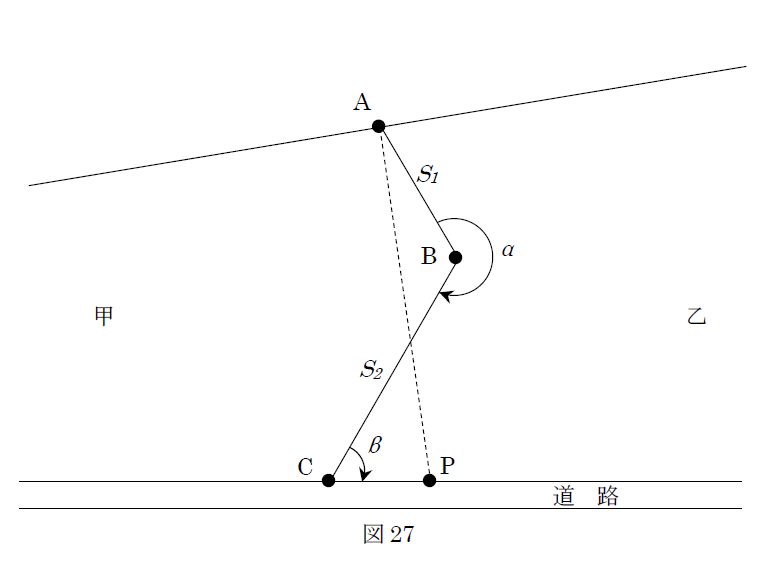
1． 14.00 m 2． 14.50 m 3． 15.00 m 4． 15.50 m 5． 16.00 m
正答は3です。
解説していきます。
この問題は、土地の境界を整正するために設置する新点と既知点の距離を求める問題です。
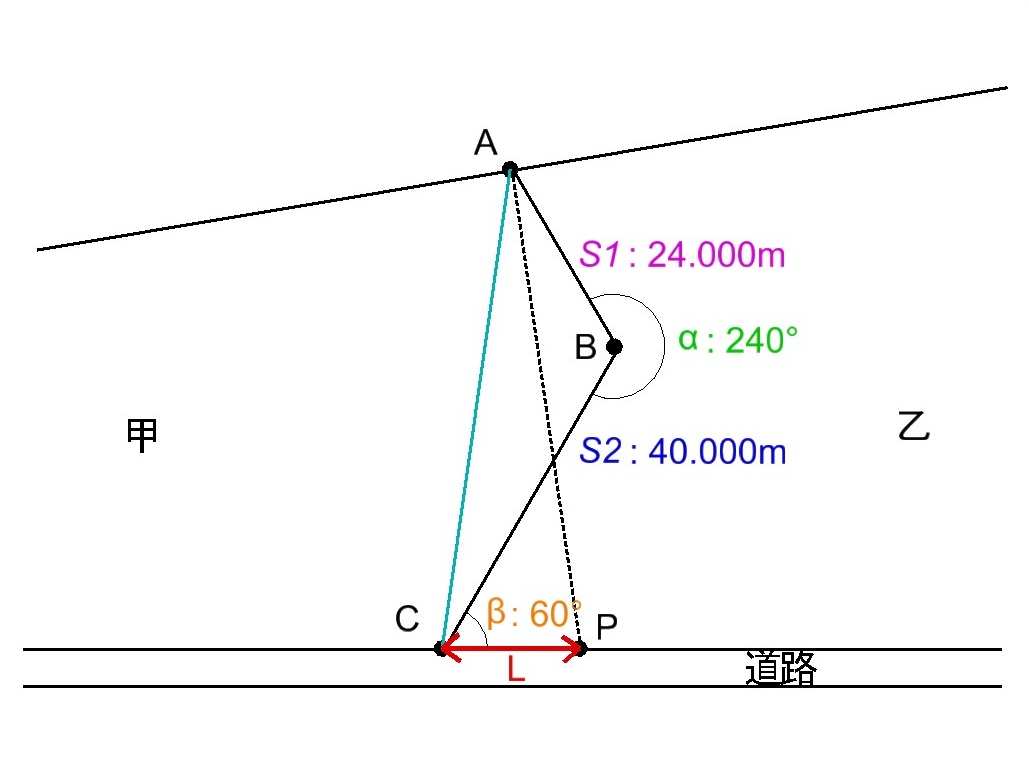
図27を参考にして、わかりやすいように点A、C間に補助線を引いた図を載せます。
図に記載されているように、以降点P、C間の距離をLとします。三角形ABCと三角形APCの面積が等しくなる場合のLが答えとなります。
まず、三角形ABCの面積Sを求めます。sinを用いた三角形の面積の公式より、
…(1)
続いて、点Cの座標を(0, 0)とし、図下部の道路をY軸と平行として、点A、点Pの相対座標を求めます。
点Pの相対座標ですが、点CとY軸に平行な位置となるため、
…(2)となります。
次に、点Aの相対座標です。こちらは与えられた数値から計算していきます。
ベクトルを用いると
…(3)とおけるため、右辺のそれぞれのベクトルの成分を求めていきます。三角関数の値は巻末の関数表から引用しています。
…(4)
…(5)
(3)、(4)、(5)より、
となり、点Aの相対座標は
…(6)となります。
(2)、(6)と座標法を使って三角形APCの面積S’の式を求めます。
…(7)
(1)、(7)より、三角形ABCと三角形APCの面積が等しくなるには
となればよいので、これをLについて解くと、
となるため、答えは3と導けます。
今回、冒頭で三角形ABCの面積を求める際にsinを使っていますが、点A、Bの相対座標を求めてから座標法を用いても問題なく解けます。
土地の境界の整正についての問題は年により多少形式は変わりますが、座標法を用いることが前提のものばかりなので、馴染みのない方はこれを機に覚えておくことをお勧めします。
No.27の解説は以上です。
また、H29年度午前の問題の解説は今回で終了となります。
ご覧いただき、ありがとうございます。
お忙しいところ、早々にご返答いただきまして、ありがとうございます。
H25年No27の件です。
下記のような結果になってしまします。
↑CA=↑CB+↑BAで、（↑はベクトルのつもりです）
↑CB＝（S2×SIN45°，S2×COS45°）
＝（12.500×0.707，12.500×0.707）
＝（8.8375，8.8375）
↑BA＝（S1×SIN90°，S1×COS90°）
＝（10.500×1，10.500×0）
＝（10.500，0）
↑CA＝（8.8375+10.500，8.8375+0）
＝（19.3375，8.8375）
A(19.3375，8.8375)，P(0，L)，C(0，0)として△ACPの面積S’を求める座標法の式に代入し、整理すると
S’＝9.66875L
S’が△ABCの面積S＝1/2（S1×S2×SIN90°）＝65.625と同値であることより
9.66875L＝65.625
L＝6.787
という結果になってしまうのです。
思い違い等で、何かが違っていると思うのですが自分ではよくわかりません。
再度のご教授をよろしくお願いいたします。
詳細なご返信、ありがとうございます。
解説記事の内容が不十分であったようで、申し訳ございません。
今回の場合は角度と大きさを用いて複数にまたがるベクトルの成分を求めております。
この場合、すべてのベクトルについて、角度は同一の軸及び方向を基準にしなければ統一された成分が求められません。
解説記事のH29年No27では偶然ベクトルCBとベクトルBAのなす角が120度になっておりますが、こちらで用いている角度の値は、
ベクトルCPとベクトルBAのなす角の値です。
ベクトルPCでなくベクトルCPを用いているのは、角βと方向を合わせているためです。
同様に、H25年No27についてもベクトルCPとベクトルBAのなす角を求めると、135度となります。
こちらを用いて、再度計算してみていただけますでしょうか。
よろしくお願いいたします。
再度のご返信ありがとうございます。
そういうことだったのですね。よくわかりました。
こちら様のH29No27の解説を拝読させていただきまして、類題練習としてH22No27とH25No27に挑戦しました。H22No27はスムーズに正解まで行き着いたのですが、H25No27は、何度見直しても正解できず、思い余って質問させていただきました次第です。
H22No27は偶然にもH29No27と同様に、α＝240°、β＝60°だったのですね。
それで正解しただけだったのですね。
ベクトル部分の解説を理解していなかったようで、お恥ずかしいばかりです。
この度は、お忙しいところ何度もご教授いただきまして、本当にありがとうございました。
失礼いたします。
わかりやすい解説ありがとうございます。
わかりやすい解説をありがとうございます。
ところで、ここで解説されておられる「座標法を使用した手法」で、H25年No27の問題に挑戦したのですが、正解までたどり着けません。
大変恐縮ですが、H25年No27も解説していただけないでしょうか。
よろしくお願いします。
コメントありがとうございます。
ご提示頂いたH25年のNo27について確認いたしましたところ、こちらの記事と同様の手順で解を導くことが可能でした。
おそらくですが、点Aの、点Cからの相対座標を求める箇所についてお困りでしょうか。
H25年のNo27についても、そのままではわかりづらいのですが、図を回転させることでH29年No27の図と似た状態になります。
また、この手順では面積を求めるために相対座標を設定しているため、図は上下を反転させても問題なく使用できます。
その他の箇所でお困りの際、また、こちらの返信がわかりづらく補足が必要でありましたら、再度ご返信いただけますでしょうか。
お手数をおかけしますが、よろしくお願いいたします。