測量士試験の過去問題を解くシリーズ、H29年度試験版の第11回です。

今回はH29年度午前No.25の問題を解いていきます。

[H29-午前No.25 問題]
図25 のように，道路の新設を計画している。新設する道路PA ～ PGは，同じクロソイドパラメータのクロソイド曲線と同じ半径の円曲線を組み合わせたもので，点PA，PD及びPGはクロソイド曲線始点，点PB，PC，PE 及びPFはクロソイド曲線終点，PB ～ PC 及びPE ～ PF は円曲線である。
新設する道路PA ～ PGの路線長は幾らか。最も近いものを次の中から選べ。
ただし，円曲線半径R = 280 m，クロソイドパラメータA = 230 m，交角I = 90 °とする。
また，円周率π= 3.142 とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。



1． 1,134 m
2． 1,190 m
3． 1,258 m
4． 1,382 m
5． 1,506 m

正答は3です。

解説していきます。

この問題は、クロソイド曲線が使われている新設する道路の路線長を、与えられたパラメータから求めるものです。
図25を参考に、色付けして値を書き込んだ図を作成しました。

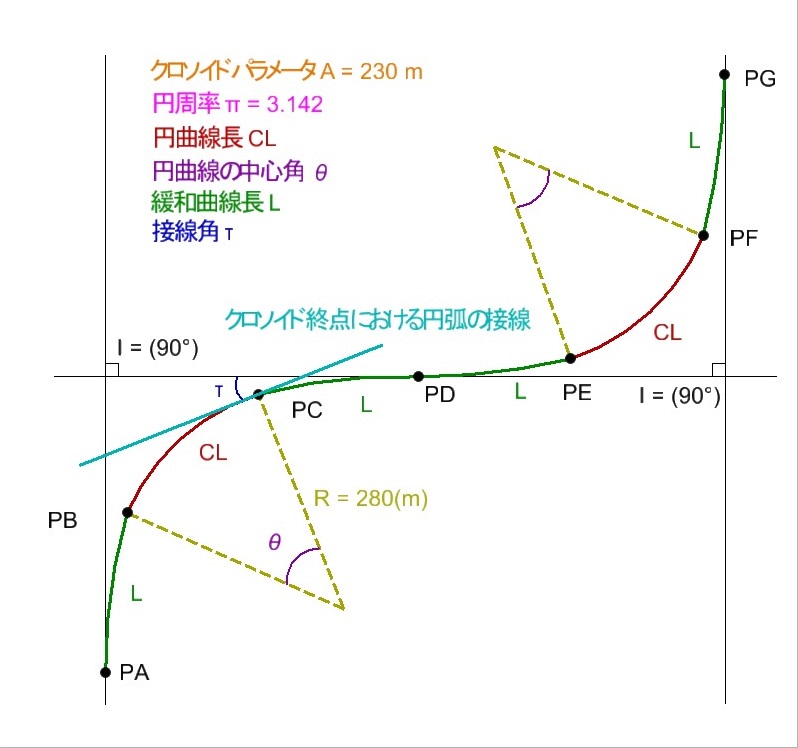
この問題の新設する道路は、同じ基本形クロソイドを2つ繋げているだけなので、基本通り公式を用いて計算していきます。
まず、クロソイドの公式より、
…(1)

続いて、クロソイドの公式および、(1)より、

ラジアンで求められるので、これを角度(degree)に変換すると、
…(2)

次に、円曲線長CLを求めます。CLは半径R、中心核Θの円弧なので、(2)より、

…(3)

(1)、(3)より、新設する道路の路線長は、

と求められ、最も近い値を示す3が正答となります。

クロソイド曲線の問題は、午前には必ず出題されている印象です。今回の問題のように、必要な公式を暗記していれば計算自体は複雑なことはないと思われますので、押さえておきたいところです。
概ね似た問題が多いので、苦手意識のある方も過去問等をまず解いてみることをお勧めします。

No.25の解説は以上です。