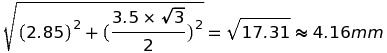測量士試験の過去問題を解くシリーズH28年度第7回目です。
今回はH28年度午前No.13の問題を解いていきます。
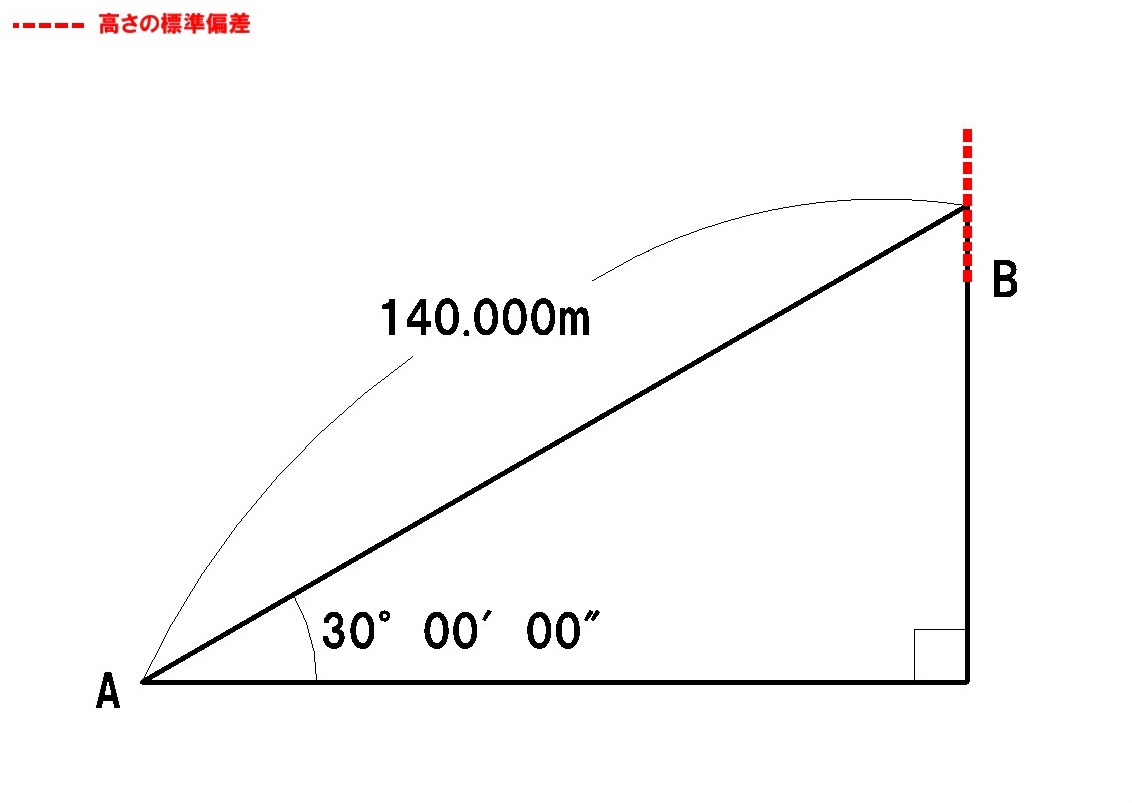
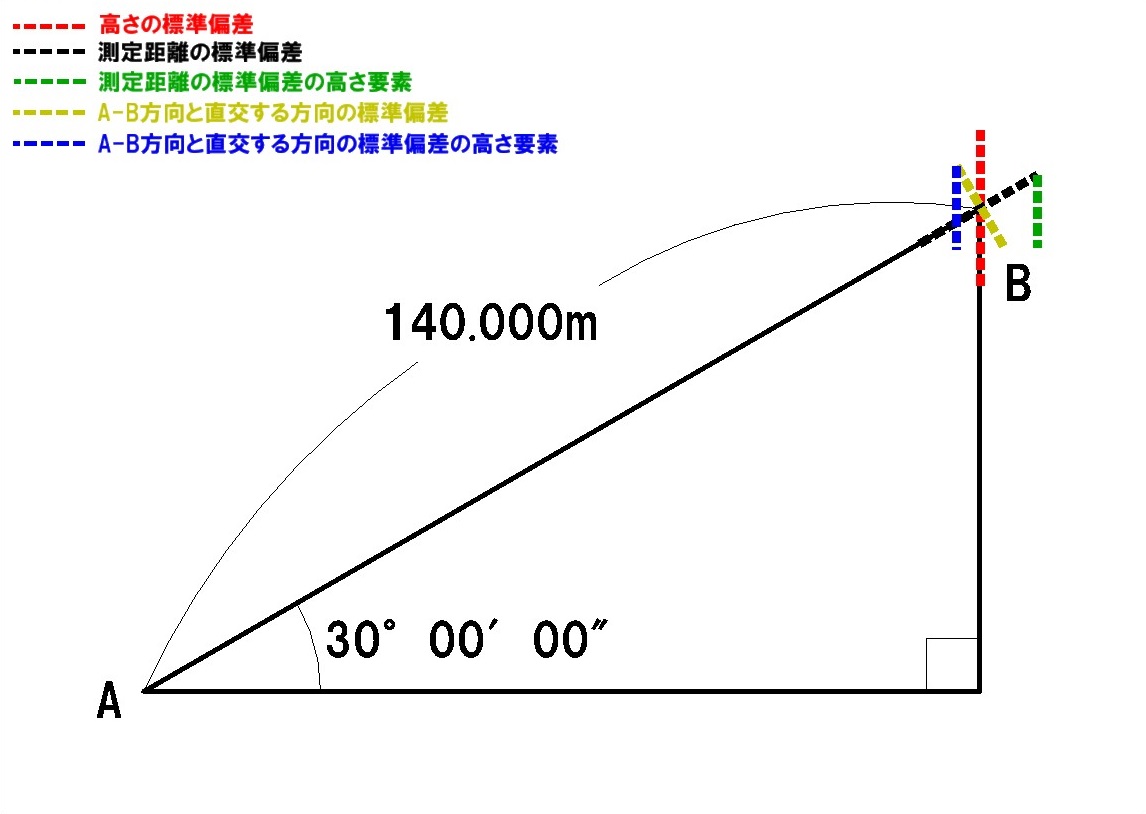
[H28-午前No.13 問題] トータルステーション(以下「TS」という。)を用いて,放射法により標高を求めたい。既知点Aから求点BをTSで観測したところ,測定距離140.000m,高低角30°00′00″を得た。使用したTSの距離測定の精度(標準偏差)が5mm+5×10-6D(Dは測定距離),角度測定の精度(標準偏差)が5″の場合,求点Bの標高の計算結果の精度(標準偏差)は幾らか。最も近いものを次の中から選べ。 ただし,TSによる距離測定と角度測定はお互いに影響を与えないものとし,その他の誤差は無視してよいものとする。また,角度1ラジアンは,(2×105)″とする。 なお,関数の値が必要な場合は,巻末の関数票を使用すること。 1. 3.0mm 2. 3.3mm 3. 4.2mm 4. 5.7mm 5. 5.9mm
この問題は、測定距離と高低角、および角度・距離それぞれの標準偏差から、高さの標準偏差を求める計算問題です。
問題中に図はありませんが、測定距離を斜辺、高低角を鋭角とした直角三角形をイメージすると考えやすくなります。
(実際の標準偏差は図中の見た目より非常に小さい値になります。)
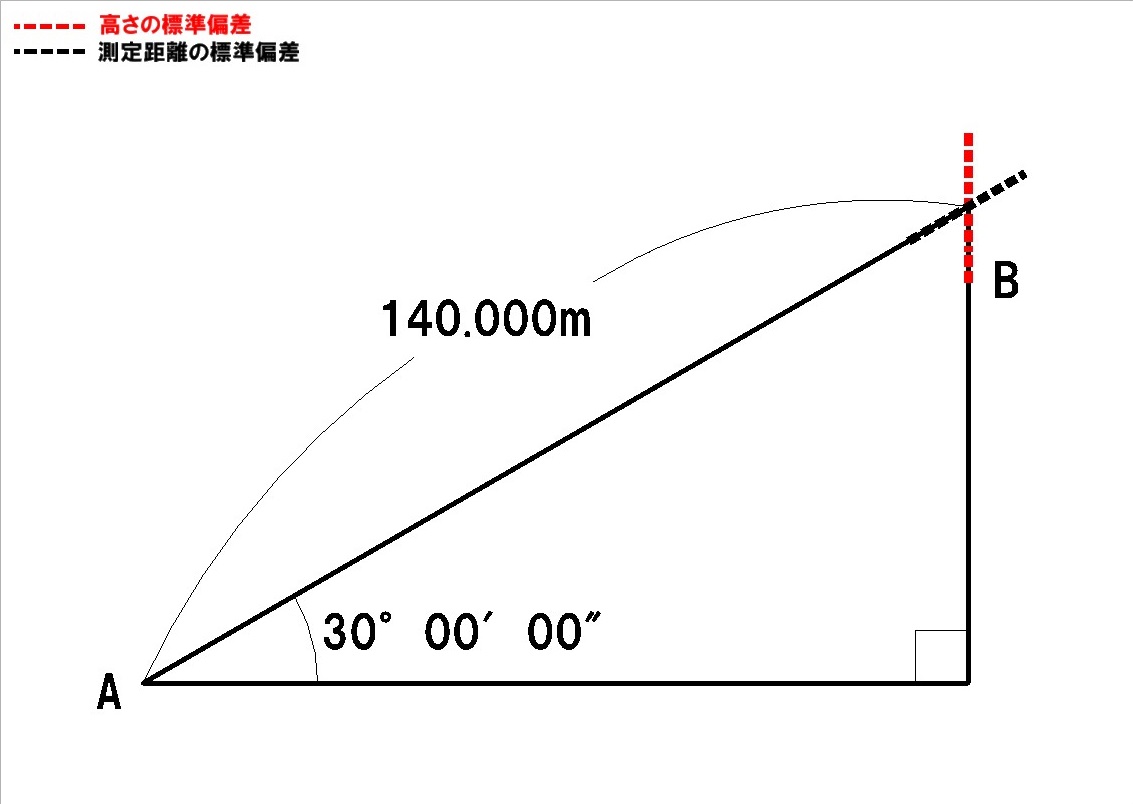
まず、測定距離と距離測定の精度から、A-B方向の距離測定の標準偏差を求めます。
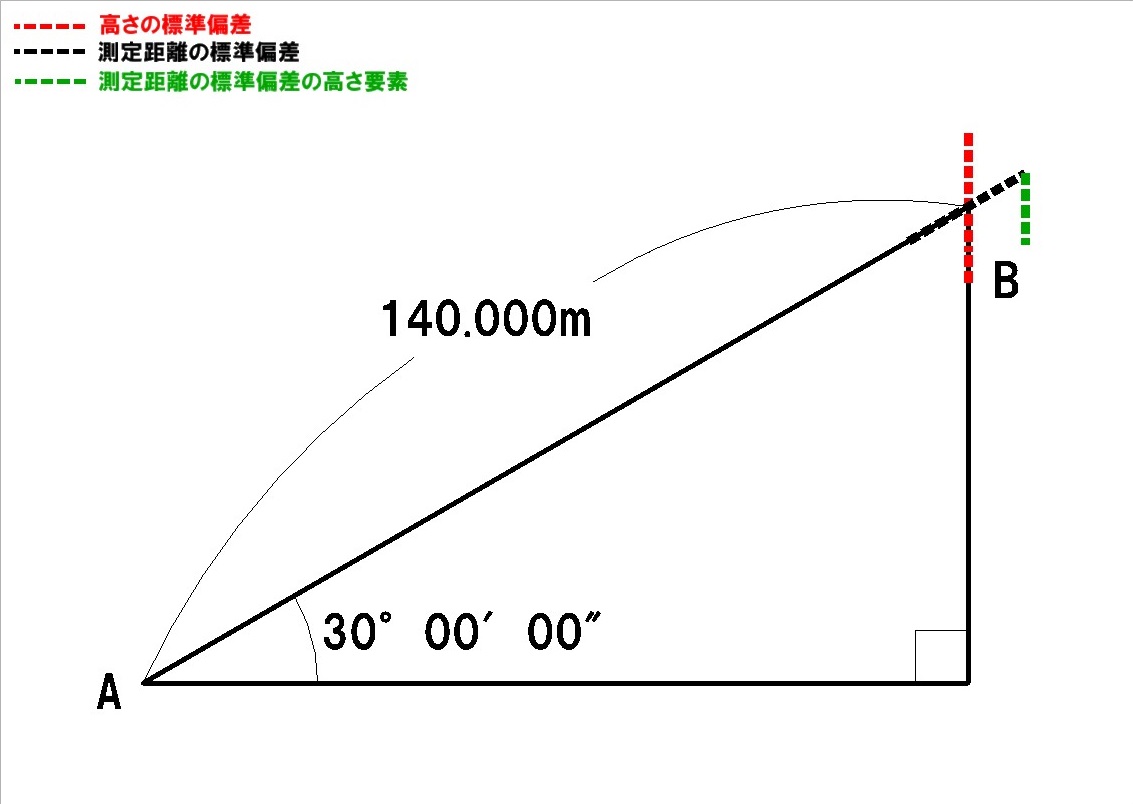
続いて、この値(5.70mm)から、高低角を用いて高さ(標高)方向の要素を取り出します。
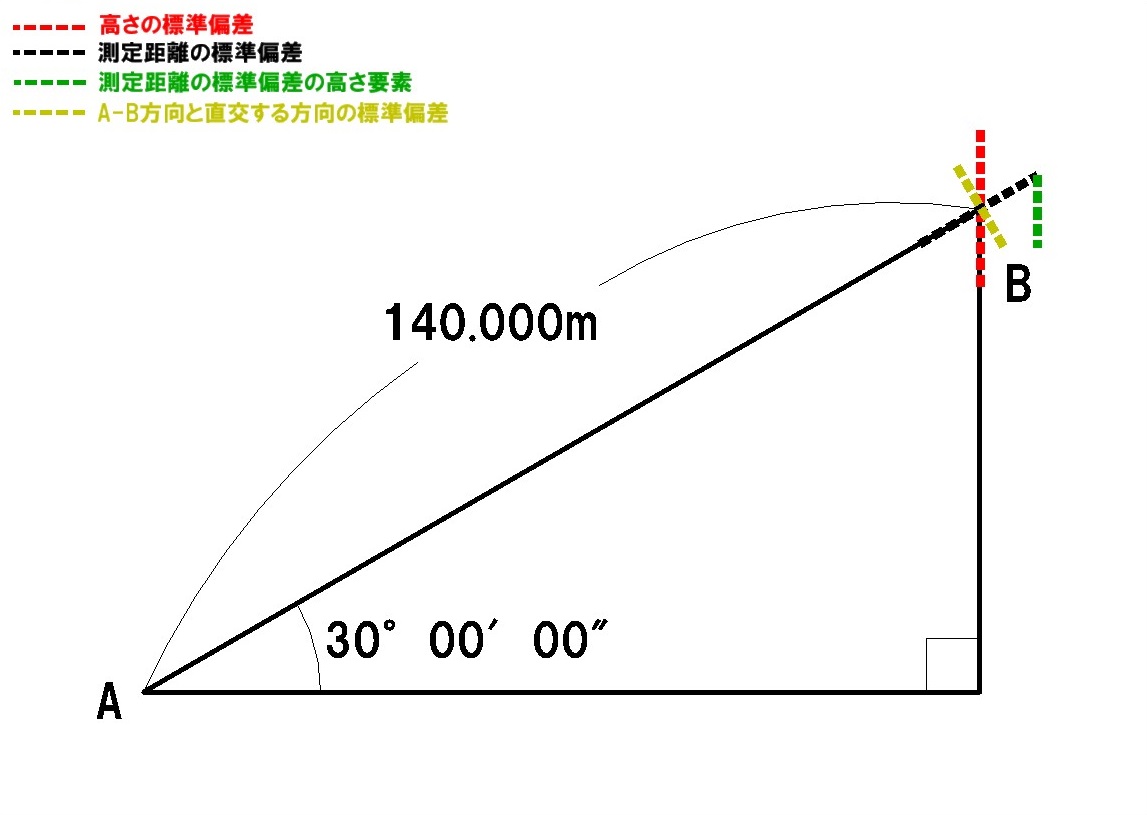
次に、測定距離と角度測定の標準偏差から、A-B方向と直交する方向の標準偏差を求めます。
(このとき、角度測定の標準偏差5″という値は非常に小さいので、これを最小の角とした直角三角形を考え、その角の対辺の長さををA-B方向と直交する方向の標準偏差の近似値として求めていきます)
続いて、この値(3.5mm)から、高低角を用いて高さ方向の要素を取り出します。
最後に、それぞれの高さ方向の要素を足し合わせて総合した高さの標準偏差を求めます。
このとき、測量で計測された値を用いて計算した値の和を求めるので、誤差伝播の法則より、
となります。
この値に最も近いのは3の4.2mm、よって答えは3。
基本的には三角関数を用いた計算が主になる問題です。
答えの値を見ると、単位の変換や桁数の違いには気づきやすい印象ですが、最後の誤差伝播の計算を忘れないように気を付けてください。
No.13の解説は以上です。