測量士試験の過去問題を解くシリーズH28年度第4回目です。
今回はH28年度午前No.5の問題を解いていきます。
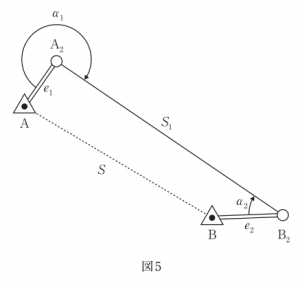
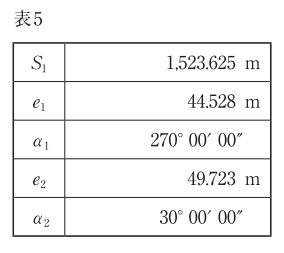
[H28-午前No.5 問題] 図5に示すように,基準点A,B間の距離を測定しようとしたところ,障害物があったため,それぞれ偏心点A2,B2に偏心して観測を行った。観測により得られた値は,表5のとおりである。基準点A,B間の基準面上の距離Sは幾らか。最も近いものを次の中から選べ。 ただし,α1,α2は偏心角,e1,e2は偏心距離,S1は偏心点A2,B2間の距離である。また,距離はすべて基準表面上の距離に補正されているものとする。 なお,関数の値が必要な場合は、巻末の関数表を使用すること。 1. 1480.103m(≒√2190706m) 2. 1480.564m(≒√2192070m) 3. 1480.694m(≒√2192455m) 4. 1481.024m(≒√2193433m) 5. 1482.725m(≒√2198473m)
示されている図と表は以下です。
(H28年度測量士試験問題集午前No.5から引用)
この問題は、相互偏心を求める問題です。
作業規程の準則(国土地理院ウェブサイト)の付録6 計算式集内の基準点測量の2.2.3 に記載されている式を覚えていれば、あとは多少の計算で解答できます。
この問題では偏心点間の距離S’(問題中の表記S1) の値が既知であり、 測点間の距離S(問題中の表記S)を求めるので、
の式を使います。
実際に解いてみます。まず、三角関数を問題用紙の関数票に従って実数にすると、
となります。これらと表の値を式に代入すると、
となり、正答は3となります。
また、この問題は、角AA2B2(360° – α1) = 90°、かつα2 = 30°なので、定番の直角三角形の辺の長さの比や三平方の定理を使えば上記の式を覚えていなくとも比較的簡単な計算で解くことができます。
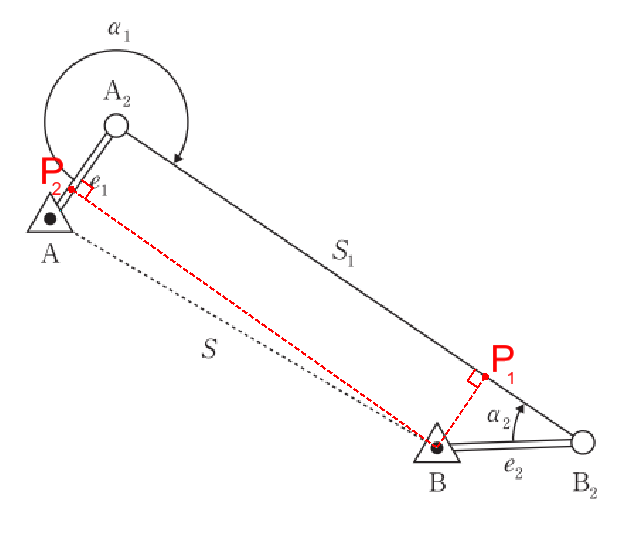
以下に別解を書いていきます。
まず、点BからS1に垂線を引き、交点をP1とします。
また、点Bからe1に垂線を引き、交点をP2とします。
すると、四角形BP1P2A2は直方体になり、
が成り立ちます。ここで辺P2A2 = 辺BP1を求めると、α2 = 30°および角BP1B2 = 90°より
となります。また、辺BP2 = 辺P1A2を求めると、
これらと、三平方の定理より、
と、求められます。
前者の解法よりやや手間は多いですが、こちらは中学くらいの数学で習う公式だけで解くことができます。
No.5の解説は以上です。

作業規定の付録6の計算式でやると
S=√( S ′-e1cosα1-e2cosα2)2+(e1sinα1+e2sinα2)2
とありますが、この問題では
S=√( S ′-e1cosα1-e2cosα2)2+(e1sinα1-e2sinα2)2
となっており、うしろの符号が変わってしまうのはなぜなのでしょうか?
コメントありがとうございます。
数式の記号を間違って記載しておりました。
ご迷惑をおかけして申し訳ございません。
該当箇所を修正いたしましたので、改めてご覧いただけると幸いです。