測量士試験の過去問題を解くシリーズH28年度第11回目です。
今回はH28年度午前No.27の問題を解いていきます。
[H28-午前No.27 問題] 図27は,境界点E,F,Gを順に直線で結んだ境界線で区切られた甲及び乙の土地を表したものであり,土地を構成する各境界点の平面直角座標系における座標値は次のページの表27のとおりである。甲及び乙のそれぞれの土地の面積を変えずに,境界点P,Qを設置して直線PQで区切られた土地に新たに区割りする場合,点QのY座標値は幾らか。最も近いものを次のページの中から選べ。 ただし,境界点Pは,甲及び乙の土地の道路に接している長さが等しくなる位置(AP=PD)とする。 なお,関数の値が必要な場合は,巻末の関数票を使用すること。
1. + 11034.00m 2. + 11034.40m 3. + 11034.80m 4. + 11035.20m 5. + 11035.60m
この問題は、全体を既存の分割線で二分している状態から、個々の面積を変えないように分割線を新設する図形の計算問題です。
五角形ABEFGと四角形ABQPの面積が等しくなる点Qを求め、そのY座標を求めていきます。
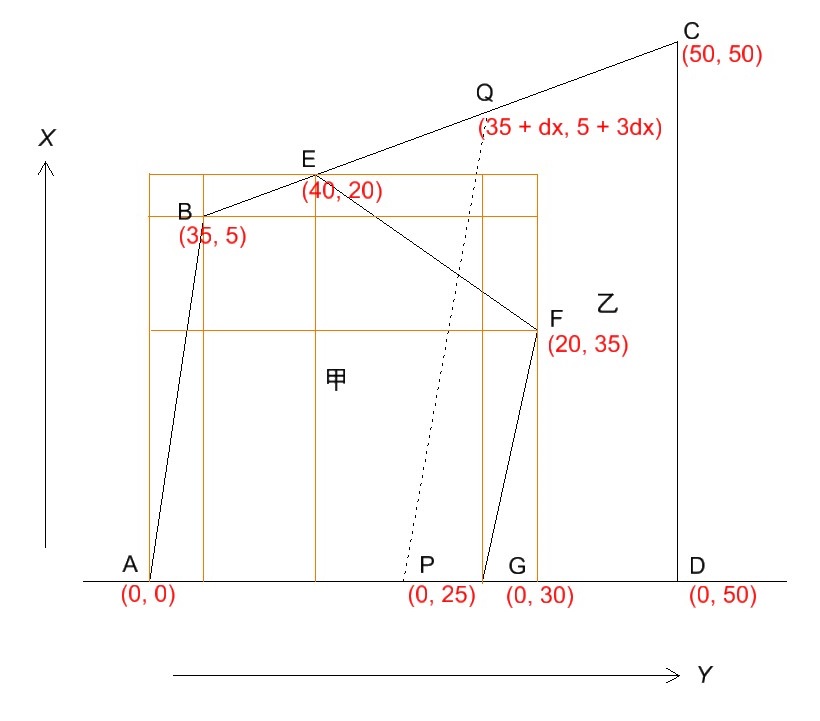
まず、図27・表27から、点Aの座標を(0, 0)とした点座標(X、Yの順、単位はm)を記入し、点A, B, E, F, Gについて、X軸・Y軸に垂直な補助線を引いた図を描きます。
また、点Qは直線BC上にあり、この直線の傾きは![]() となるので、点Bを基準としたX軸方向の値をdxとおくと、Y軸方向の値は3dxとなります。この代数を用いて点Qの座標を記入しています。
となるので、点Bを基準としたX軸方向の値をdxとおくと、Y軸方向の値は3dxとなります。この代数を用いて点Qの座標を記入しています。
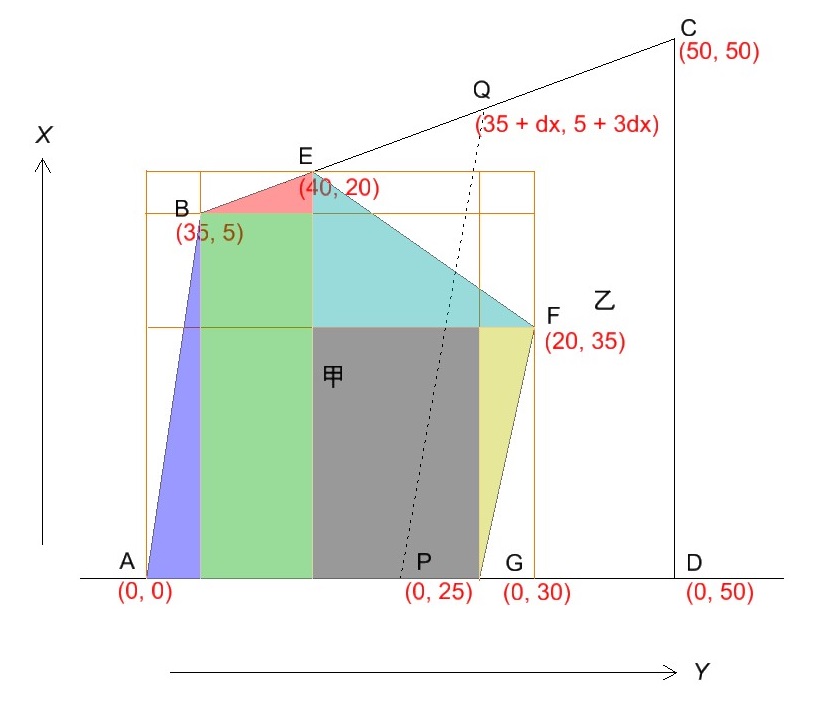
これを参考に、まず五角形ABEFGの面積を求めます。
こんな形で単純に計算できるよう分割すると求めやすくなります。
赤色の三角形の面積は![]()
青色の三角形の面積は![]()
緑色の四角形の面積は![]()
水色の三角形の面積は![]()
灰色の四角形の面積は![]()
黄色の三角形の面積は![]()
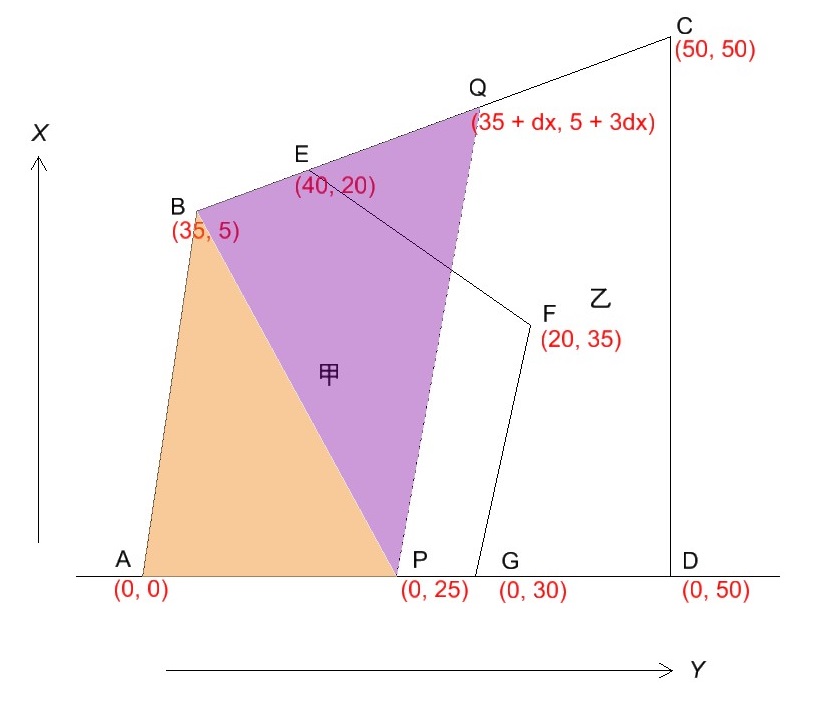
続いて、四角形ABQPの面積を表す式をたてます。
こちらは、上記のように二分して考えます。
橙色の三角形の面積は![]() ・・・(2)
・・・(2)
紫色の三角形の面積は、二辺とその間の角を用いた公式より、
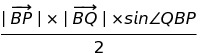 ・・・(3)
・・・(3)
とできるため、これを解いていきます。
以上より、(1) = (3) + (4)となるdxを求めます。
![]()
となります。
このdxは点Bを基準とした値なので、正しい点QのY座標は、
![]()
となり、正答は2となります。
少し長くなりましたが、基本的に難しくない公式等で解けています。
三角関数やベクトルに関しては、図形問題に使う機会が多いので、自信のない方は少し確認してみてください。
No.27の解説は以上です。

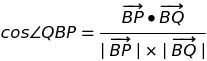
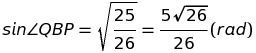
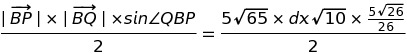
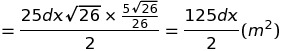
今年測量士の資格を取得してくれと言われ勉強を始めました。
このGEO Solutions 技術情報がものすごく解説が良くできているのでいつも参考にさせてもらっています。
一つ質問なのですが、H28年度測量士試験No,27の問題で
座標Aが(0.0)座標Dが(0.50)ADの長さが50mとありますがどこから50mという数値が出てくるのでしょうか?
初歩的な質問で申し訳ございません。
解説お願いします。
コメントありがとうございます。
ご質問承りました。
こちらの記事中に使用している図中の各点座標は、図27・表27をもとに点Aの座標をX、Yそれぞれ0mとなるよう平行移動したものです。
mという単位につきましては、表27に準じております。