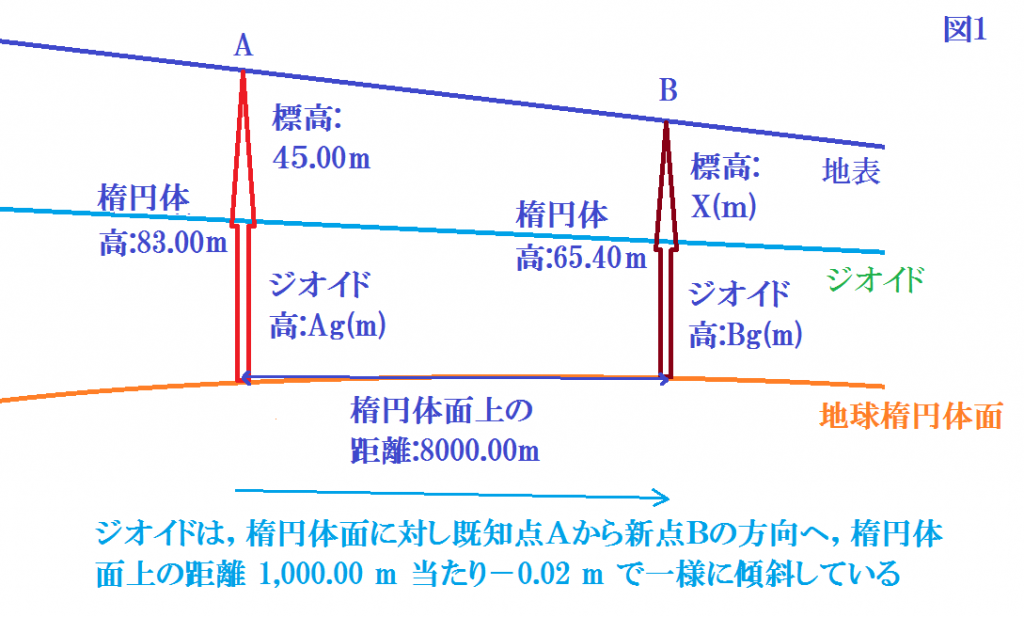
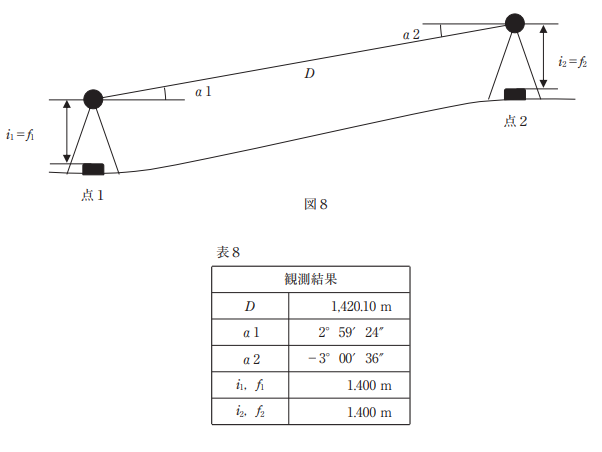
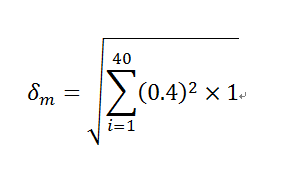測量士試験の過去問題を解くシリーズ、令和元年度試験版の第8回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

〔No．17〕 　　
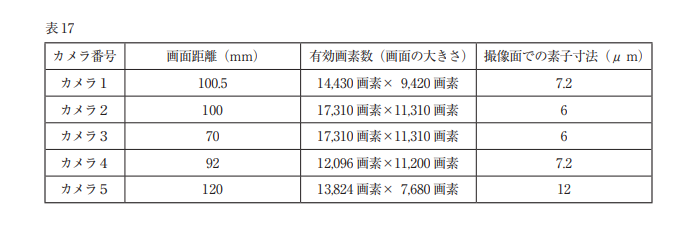
　　　表 17 に示す５種類のデジタル航空カメラを用いて空中写真の撮影を行う場合，同じ地上画素寸法になるようにコースを設計すると，撮影対地高度が最も高くなるカメラはどれか。次の中から選べ。
　　　ただし，表 17 に示すもの以外の条件は同一とする。

1. カメラ１
2. カメラ２
3. カメラ３
4. カメラ４
5. カメラ５

解答は2です。以下解説して行きます。

下記17-2は解説のために作成致しました。変数はそれぞれ、
l=写真の範囲の距離
d=撮像面での素子寸法
f=画面距離
H=撮影対地高度
D=素子寸法に対応する地上距離
L=写真の範囲に対応する地上距離
です。

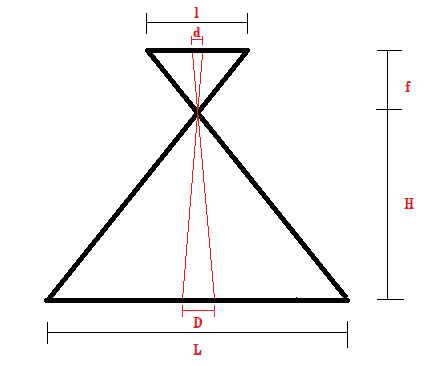
空中写真の幾何学的性質から、
f/H=l/L … ①
が成り立ちます。同様に、
f/H=d/D … ②
が成り立ちます。

②から、 カメラのH( 撮影対地高度)は、
H=f ×D / d … ③
で求める事ができます。

カメラ１からカメラ５までのD（地上画素寸法 ）が同じ
という条件が与えられていますので、
カメラ１からカメラ５までのH( 撮影対地高度)は、
f / dの大きさによって決定する事ができます。

問の表17から d, f の値が与えられまので、カメラ１からカメラ５までのf/dの値を求めます。値の大小の比較を行うだけですので単位を合わせなくても構いません。

カメラ１ の撮影対地高度の比 (f/d) ＝ 100.5 / 7.2 ≒ 13.96
カメラ２ の撮影対地高度の比 (f/d) ＝ 100 / 6 ≒ 16.67
カメラ３ の撮影対地高度の比 (f/d) ＝ 70 / 6 ≒ 11.67
カメラ４ の撮影対地高度の比 (f/d) ＝ 92 / 7.2 ≒ 12.78
カメラ５ の撮影対地高度の比 (f/d) ＝ 120 / 12 ≒ 10

よって上の結果から、 撮影対地高度の比 (f/d) が最も大きいのは２となります。
以上です。

測量士試験の過去問題を解くシリーズ、令和元年度試験版の第7回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

 〔No．14〕
　　　新たに完成した宅地造成地の既成図を数値地形図データの修正に用いることとした。この既成図の図 郭四隅の点Ａ，Ｂ，Ｃ，Ｄには，図 14－1 に示す平面直角座標系（平成 14 年国土交通省告示第 9 号） における座標値が記載されていた。また，これをスキャナにより数値化し，コンピュータソフトウェア を用いてスクリーンモニター上で図郭の四隅の点を計測したところ，図 14－2 に示す座標値を得た。
　　　この数値化された既成図を，式 14－1 の変換式を使って補正し，数値地形図データとの位置合わせ を行いたい。変換係数 a，b，c，d を最小二乗法により求めるための観測方程式が次のページの式 14－ 2 である。  ア  ～  エ  に入る数値の組合せとして正しいものはどれか。次のページの中 から選べ。
　　　ただし，変換式の X，Y は既成図の座標値，x，y はスクリーンモニター上で計測した座標値，a，b， c，d は変換係数とし，観測方程式の VAX，VBX，VCX，VDX は点 A，B，C，D 各点の平面直角座標系に おける X 座標の残差を，VAY，VBY，VCY，VDY は Y 座標の残差を示すものとする。

解答は2です。以下解説して行きます。

図14-2の B(3, 393) は 、図2の式14-2から VBXと VBY を求めるための
図1の式14-1における a, b, c, d の値は、a=3, b=393, c=1, d=1
となります。

図14-2の C(0, 0) は 、図2の式14-2 から VCXと VCY を求めるための
図1の式14-1における a, b, c, d の値は、a=0, b=0, c=1, d=1
となります。

図14-2の D(623, -2)は、図2の式14-2 から VDXとVDYを求めるための
図1の式14-1における a, b, c, d の値は、a=623, b=-2, c=1, d=1
となります。

図14-2の A(623, 390)は、図2の式14-2 から VAXとVAYを求めるための
図1の式14-1における a, b, c, d, の値は、B, C, Dと同様に当てはめて、
a=623, b=390, c=1, d=1 となり、上記表1では、
2.の ア=-623, イ=390, ウ=390, エ=623
が該当します。

以上です。

測量士試験の過去問題を解くシリーズ、令和元年度試験版の第6回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

 〔No．13〕 　　

　視準距離を等しく 45 m として，路線長 1.8 km の水準点Ａ，Ｂ間の水準測量を実施した。1測点に おける1視準1読定の観測の精度（標準偏差）が 0.4 mm であるとき，観測により求められる水準点 Ａ，Ｂ間の片道の観測高低差の精度（標準偏差）は幾らか。最も近いものを次の中から選べ。 　　　
　ただし，1測点では，後視及び前視の観測を1回ずつ，1視準1読定で行ったものとする。
　なお，関数の値が必要な場合は，巻末の関数表を使用すること。 　　

1. 1.0 mm 　　
2. 1.3 mm
3. 1.8 mm
4. 2.5 mm
5. 3.6 mm

（引用終了）

正解は4です。 以下解説して行きます。

何箇所で測定されるかを調べます。
路線長 1.8 km の水準点Ａ，Ｂ間 で、後視及び前視がそれぞれ視準距離45mで行われますので、
S = 1800 ÷ 45 = 40 … ①
40箇所となります。

与えられた 条件から各測定値間の相関はないものとみなせますので、下記の誤差伝搬の法則を適用します。

上式の 偏微分の項は全て『1』となります。
１測点に おける１視準１読定の観測 の精度 （標準偏差） は 『0.4』 と与えられているため、 全ての δi は 0.4となります。
上記①から、n = 40となります。
よって、各々の値を代入すると下記の様になります。

よって、
δｍ =√(40 ×(0.4 ×0.4)) ≒ 2.53
となります。
　　　　　　　　　　　　　　　
最も近い値は2.5ですので、解答は4となります。

以上です。

測量士試験の過去問題を解くシリーズ、令和元年度試験版の第5回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

[R 1-午前No.10問題] （以下引用開始）

 〔No．10〕

　既知点Ａ及び新点Ｂにおいて GNSS 測量機を用いた測量を行い，既知点Ａから新点Ｂまでの楕円体 面上の距離 8,000.00 m，新点Ｂの楕円体高 65.40 m の値を得た。このとき，新点Ｂの標高は幾らか。最 も近いものを次の中から選べ。 　 　ただし，既知点Ａの標高は 45.00 m，楕円体高は 83.00 m であり，ジオイドは，楕円体面に対し既知 点Ａから新点Ｂの方向へ，楕円体面上の距離 1,000.00 m 当たり－0.02 m で一様に傾斜しているものと する。 なお，関数の値が必要な場合は，巻末の関数表を使用すること。 　　

1. 　27.14 m 　　
2. 　27.24 m 　　
3. 　27.40 m
4. 　27.56 m
5. 　28.56 m

（引用終了）

正解は4です。 以下解説して行きます。

ジオイドとは、 国土地理院サイト (https://www.gsi.go.jp/) から
(以下引用開始）

水は、高いところから低いところに流れます。地図に記される高さ（標高）は、水道などのインフラ整備や、津波や洪水等から命を守る上でとても大切な情報ですが、実はその標高は地形の起伏だけでは決められません。平らに見える地表面でも、重力の分布が一様でなければ、水は重力の強い方に流れています。同じように、正確な標高を知るためには、地形の起伏を測定するだけではなく、重力の影響も考慮する必要があります。

　日本の標高の基準は、測量法で平均海面と定められています。この平均海面を仮想的に陸地へ延長した面をジオイドといいます。
　国土地理院では、重力測量や水準測量の結果などから、地球を仮想的に表した楕円体表面からジオイドまでの高さ（ジオイド高）を決めています。衛星測位で決まる高さ（楕円体高）からジオイド高を引くことで、簡単に標高を求めることができます。

（引用終了）

問を図示すると下記のようになります。

流れとして、図のAgを求めてBgを求めて、Xを求めます。

既知点Aのジオイド高:Agを求めます。
Ag=83.00m-45.00m
=38.00m

新点Bのジオイド高:Bgを求めます。
Bg=Ag+(8000.00m÷1000.00m)×(-0.02)
=38.00m-0.16
=37.84m

新点Bの標高:Xを求めます。
X=65.40m-Bg
=65.40m-37.84m
=27.56m

という事で、解答は４番となります。

以上です。

測量士試験の過去問題を解くシリーズ、令和元年度試験版の第4回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

[R 1-午前No.8 問題] （以下引用開始）

〔No．8〕
　公共測量におけるトータルステーションを用いた１級基準点測量において，図８に示すように標高23.50 m の点１と標高 97.70 m の点２の間の距離及び高低角の観測を行い，表８の観測結果を得た。Dを測定距離，α1 を点１から点２方向の高低角，α2 を点２から点１方向の高低角，i1，f1 を点１の器械高，目標高，i2，f2 を点２の器械高，目標高とするとき，点１，点２間の基準面上の距離は幾らか。最も近いものを次の中から選べ。
　ただし，地球の平均曲率半径は 6,370 km，点１，点２のジオイド高を平均した値は 40.00 m を用いるものとする。
　なお，関数の値が必要な場合は，巻末の関数表を使用すること。

1. 1,418.09 m 　　
2. 1,418.11 m
3. 1,418.13 m
4. 1,418.15 m
5. 1,418.17 m

（引用終了）

正解は3です。

基準面上の距離を求めるために、国土交通省サイトの測量機器検定基準の計算式集 付録６のP160-161にある式を引用します。
(以下引用開始)

（引用終了）

問8の文中で与えられた値を式に当てはめて行きます。
D=1420.10ｍ
H1=23.50m+1.400m=24.90m
H2=97.70m+1.400m=99.10m
α1=2°59′24″
α2=-3°00′36″
R=6370km=6370000m
Ne=40.00m

から、

S ＝ 1420.10 × cos(6/2) × 6370000 ÷ ( 6370000 + (24.90 + 99.10) / 2 + 40.00 )
＝ 1420.10 × 0.99863 × 6370000 ÷ ( 6370000 + 102.00 )
＝ 1420.10 × 0.99863 × 0.99998
＝ 1418.1545 × 0.999983
≒ 1418.13

※ cos(3°)= 0.99863 (巻末の関数表 より)

計算式を記憶していないと解きにくい問題だと思います。
以上です。