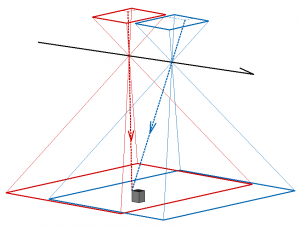
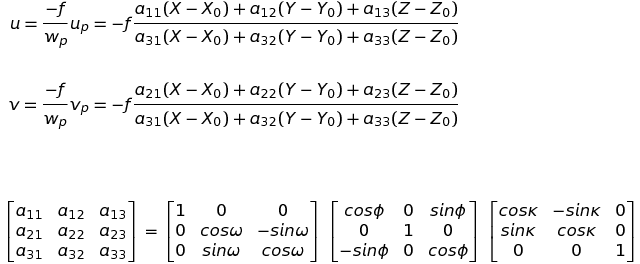写真測量夜話もとうとう10回目ということで、一区切りとすべく写真測量で最も重要な式のひとつである共線条件式を紹介していきます。

 

さて、前回は

外部標定要素は航空写真の画素位置と地理座標(緯度・経度・標高)を画素位置→地理座標の場合は12個、地理座標→画素位置の場合は6個のパラメーターで対応づけますよ、というところまでで終わっていました。

画素位置→地理座標では
(x,  y,  x’, y’) →[12個のパラメーター]→ (X, Y, Z)

地理座標→画素位置では
(X, Y, Z) →[6個のパラメーター]→ (x,  y)
(X, Y, Z) →[6個のパラメーター]→(x’,  y’)

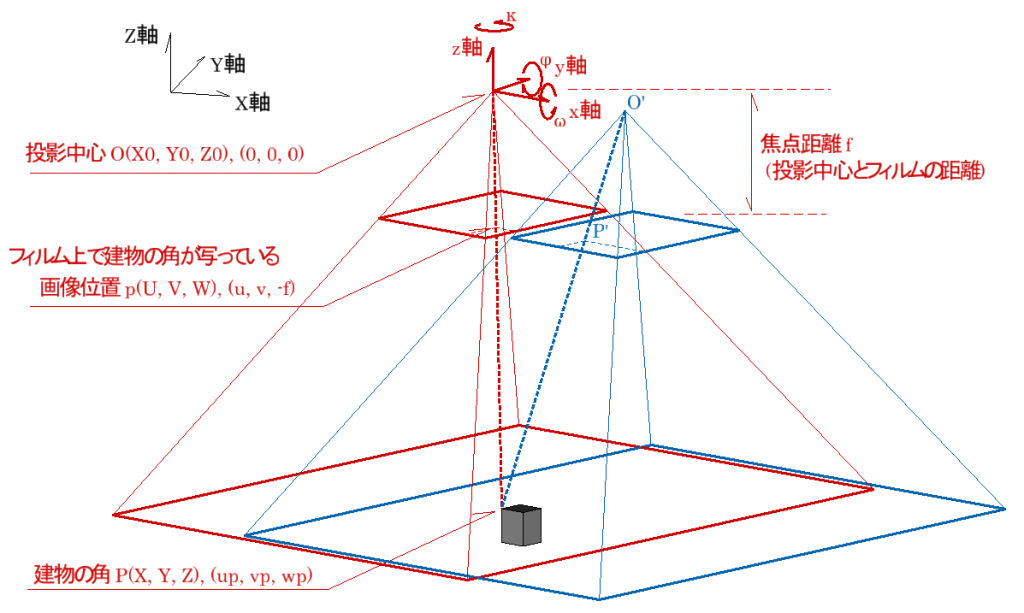
まずは、このパラメーターがおなじみの

この図上にどう表現できるか、見てみましょう。簡単のため、左側(赤線)でだけ示していきます。

 

…

 

前回でいうeasting, northing, heightは簡単ですね。砂時計のくびれた場所です。カメラの投影中心となり、画素位置、地理座標(建物の角)と併せて図示すると以下のようになります。式を示すときにeasting, northing, heightでは扱いずらいので、X0,Y0,Z0としましょう(この0とup, vp, wpのpは添字と考えて下さい)。

 

つぎに残りのomega, phi, kappa(こちらも以下ω, φ, κ)です。これは航空機の傾きでした。この場合カメラの傾きと思えばよく、もろもろ都合よく図示すると次のようになります。

 

 

…

 

急に上の逆ピラミッド部分がひっくり返って、様子が変わってしまいました。素直にカメラを思い浮かべるなら元々の形なのですが、一般的な形の数式を示したい都合上、こうします。カメラの内部標定要素としてf(焦点距離)だけは出てきてもらわないといけませんが、定数という理解でOKです。

さて、この図で見落としてはいけないことは、座標系は2つ、

 

地理座標を考えるときの座標系A(上図左)と画素位置を考えるときの座標系B(上図左右)とがある、という事です。ちなみに、図中にはO, p, Pと3点に座標をそれぞれ2つ記していますが、左側がAで、右側がBで示したものです。

そして、共線条件式というからにはもちろん最も重要な、O, p, Pは同一の直線上に存在していることを利用すると、共線条件式

を導くことができます(書くのはここがお手軽です。ありがたや。)。地理座標→画素位置の変換はこの式1組を、逆の変換は2組を使用して行うことになります。

 

…

 

とにかく最後の形だけ、という体で写真測量で重要な共線条件式を紹介しましが、導出はすっとばしてしまっています。興味を持たれた方は手ずから導いてみたり、または地理座標→画素位置/画素位置→地理座標変換を行うプログラムを書いてみたり(※1)と、是非色々試してみて下さい。

それでは、次回からは気分を変えてもっと軽いお話を。

—

※1 画素位置→地理座標と変換しようとすると、3つの数値を求めたいのに式が4つあるぞ？となります。はてさて？