測量士試験の過去問題を解くシリーズ、令和2年度試験版の第7回です。
　以下、「国土地理院」サイトの 令和2年11月22日の問題を引用して解説して行きます。
〔No.25〕

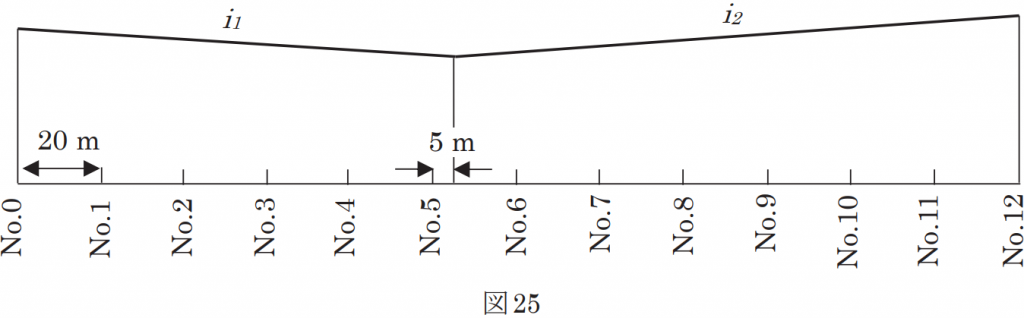
　図25に示すように，中心杭No.0からNo.12に向かう途中で縦断勾配がi ₁＝－4％からi₂＝＋4％に変移する道路がある。自動車運転の安全性の観点から，勾配の変移に伴う衝撃を緩和するため，この道路に縦断曲線を挿入したい。この道路の縦断勾配の変移する箇所が　No.5＋5 mのとき，縦断曲線の始点はどこか。最も近いものを次の中から選べ。

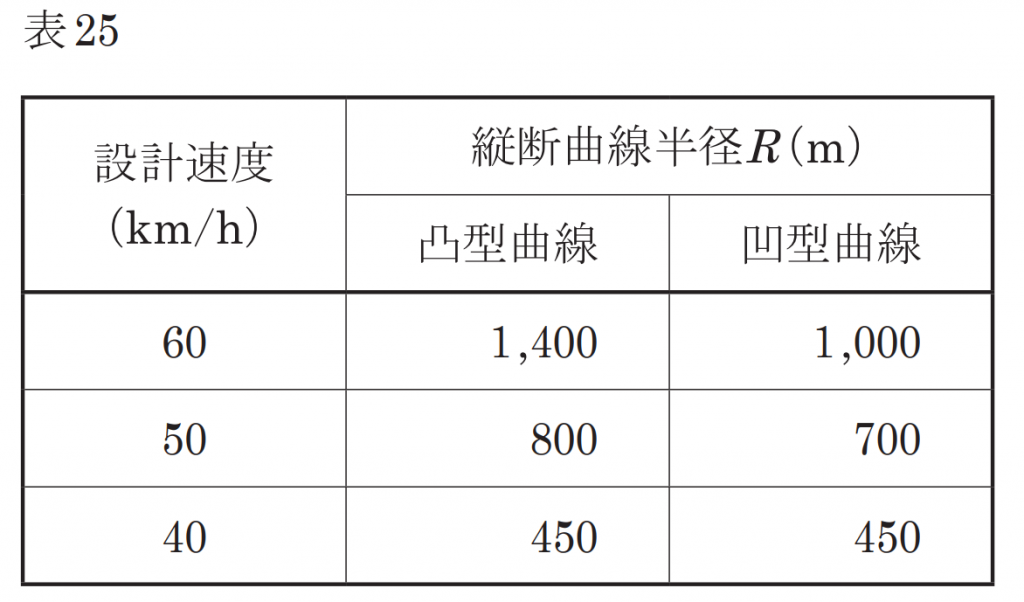
　ただし，道路の設計速度は50 km/h，中心杭間距離は20 mとし，縦断曲線半径R の数値は表25を用いる。また，変移前後の勾配の差が小さく，さらに，両勾配の絶対値が等しいことから，挿入する縦断曲線の曲線長を式25によって求め，その長さを挿入曲線の始終点間の水平距離と同一視して差し支えないものとする。

　なお，関数の値が必要な場合は，巻末の関数表を使用すること。

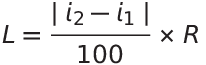
1．　No.2＋9m
2．　No.3＋5m
3．　No.3＋13m
4．　No.3＋17m
5．　No.4＋13m

解答は4です。以下、解説です。

　縦断曲線の始点を求める問題です。No5＋5地点が縦断勾配の変移する箇所=縦断曲線の中央だから、まずは縦断曲線の曲線長を求めます。縦断曲線の曲線長は式25で求めることができます。i₁とi₂は問題文中で与えられているのでRについて考えます。Rは表25より求められ、問題文中の設計速度50km/hと図25の曲線形状が凹型曲線だから縦断曲線半径Rは700mとなります。これを式25に代入して
L=(|4-(-4)|/100)×700
L=(|8|/100)×700
L=0.08×700
L=56m
縦断曲線長は56mと求められました。

縦断曲線の曲線長を縦断勾配変移点から中心に半分にすれば曲線の始点と終点が求められます。縦断勾配変移点は中心杭No.5から5ｍ進んだところなので
縦断勾配変移点=20×5+5=105
縦断勾配変移点は中心杭No.0から105mの位置にあるということになります。

縦断曲線の始点は
105-(56/2)=77
中心杭No.0から77mの位置にあります。

中心杭は20m毎に設置されているので
77÷20=3⋯17
よって始点はNo.3+17mの位置にあるため、解は4となります。