測量士試験の過去問題を解くシリーズ、令和元年度試験版の第5回です。
以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。
[R 1-午前No.10問題] (以下引用開始)
〔No.10〕
既知点A及び新点Bにおいて GNSS 測量機を用いた測量を行い,既知点Aから新点Bまでの楕円体 面上の距離 8,000.00 m,新点Bの楕円体高 65.40 m の値を得た。このとき,新点Bの標高は幾らか。最 も近いものを次の中から選べ。 ただし,既知点Aの標高は 45.00 m,楕円体高は 83.00 m であり,ジオイドは,楕円体面に対し既知 点Aから新点Bの方向へ,楕円体面上の距離 1,000.00 m 当たり-0.02 m で一様に傾斜しているものと する。 なお,関数の値が必要な場合は,巻末の関数表を使用すること。
- 27.14 m
- 27.24 m
- 27.40 m
- 27.56 m
- 28.56 m
(引用終了)
正解は4です。 以下解説して行きます。
ジオイドとは、 国土地理院サイト (https://www.gsi.go.jp/) から
(以下引用開始)
水は、高いところから低いところに流れます。地図に記される高さ(標高)は、水道などのインフラ整備や、津波や洪水等から命を守る上でとても大切な情報ですが、実はその標高は地形の起伏だけでは決められません。平らに見える地表面でも、重力の分布が一様でなければ、水は重力の強い方に流れています。同じように、正確な標高を知るためには、地形の起伏を測定するだけではなく、重力の影響も考慮する必要があります。
日本の標高の基準は、測量法で平均海面と定められています。この平均海面を仮想的に陸地へ延長した面をジオイドといいます。
国土地理院では、重力測量や水準測量の結果などから、地球を仮想的に表した楕円体表面からジオイドまでの高さ(ジオイド高)を決めています。衛星測位で決まる高さ(楕円体高)からジオイド高を引くことで、簡単に標高を求めることができます。
(引用終了)
問を図示すると下記のようになります。
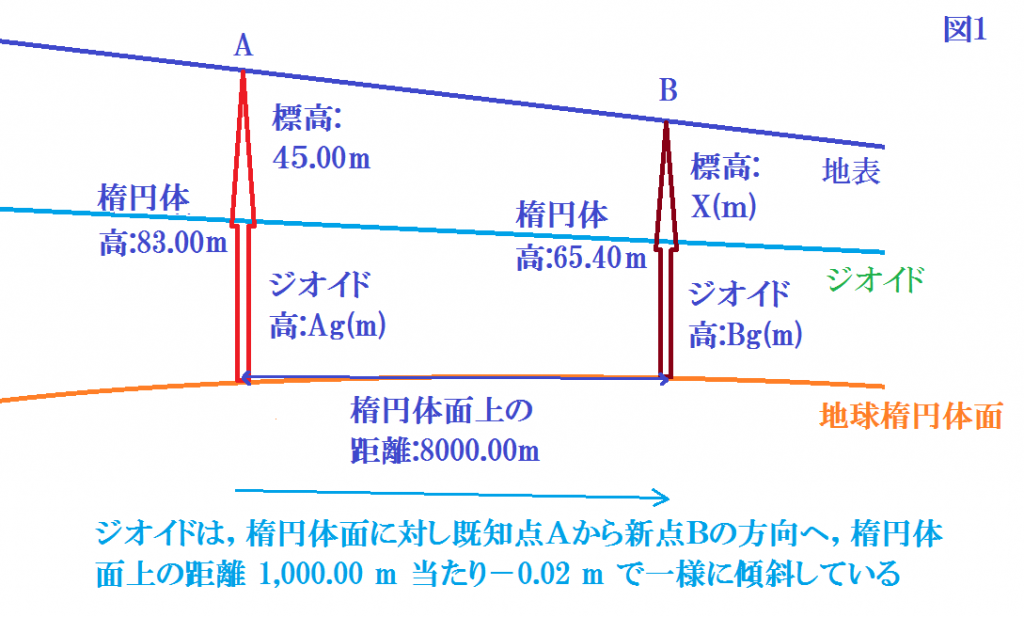
流れとして、図のAgを求めてBgを求めて、Xを求めます。
既知点Aのジオイド高:Agを求めます。
Ag=83.00m-45.00m
=38.00m
新点Bのジオイド高:Bgを求めます。
Bg=Ag+(8000.00m÷1000.00m)×(-0.02)
=38.00m-0.16
=37.84m
新点Bの標高:Xを求めます。
X=65.40m-Bg
=65.40m-37.84m
=27.56m
という事で、解答は4番となります。
以上です。

