測量士試験の過去問題を解くシリーズH28年度第5回目です。
今回はH28年度午前No.6の問題を解いていきます。
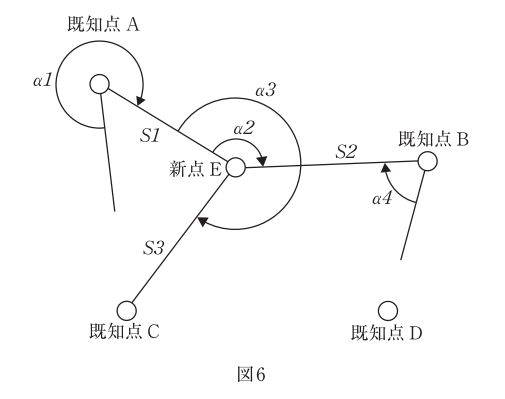
[H28-午前No.6 問題] 図6に示すように,基準点測量において結合多角方式により新点Eの水平位置を求めるために,S1~S3の距離及びα1~α4の水平角の観測を行った。表6は,観測結果による厳密水平網平均計算から求めた各観測値の残差Vと,その時に用いた重量Pを示す。 単位重量の標準偏差Mは,式6のとおり,各観測値の残差Vの二乗に重量Pをかけた総和(ΣPVV)を自由度Fで割った平方根で求められる。この網平均計算結果における単位重量の標準偏差は幾らか。最も近いものを次の中から選べ。 ただし,S1~S3の観測値の残差を角度に変換したものをVS1~VS3とし,α1~α4の観測値の残差をVα1~Vα4とする。 なお,関数の値が必要な場合は,巻末の関数票を使用すること。
1. 1.2" 2. 1.4" 3. 2.0" 4. 2.1" 5. 2.3"
この問題は、観測結果における単位重量の標準偏差(問題中のM)を求める計算問題です。
作業規程の準則(国土地理院ウェブサイト)の付録6 計算式集内の基準点測量の2.4.3 (5)に記載されている式を使います。(下記)
V : 残差のベクトル Vr : Vの転置行列 P : 観測値の重量の行列 q : 観測方程式の数 r : 方向観測の組の数 n : 新点の数
この式と式6は同じものを示しています。具体的には、
(式6) (準則計算式2.4.3 (5))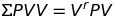
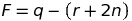
と対応しています。
では、実際に計算していきます。
まず、
こちらは問題文にも記載されているように、各観測値の残差Vの二乗に対応する重量Pをかけた値を足し合わせればよいので、
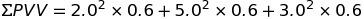
- ➀
次に、自由度
です。測量の計算において、自由度は観測値の数と未知数の数の差で示されます。
この問題での観測結果における自由度の構成要素(q,r,n)に、それぞれ何が当てはまるのか確認していきます。
まず、q (観測方程式の数)は、
残差Vを求めている式(合計7つ)および、既知点から新点への距離を求める式(合計3つ)をたしあわせた、10。
続いて、r(方向観測の組の数)は、方向観測を行っている点の数(合計3つ)。
最後に、n(新点の数)は1つ。(式中で×2されているのは、1点につきx座標の値とy座標の値がそれぞれ未知数として数えられるため)
これらの値を代入して計算すると、
- ②
➀、②より、単位重量の標準偏差Mは
となり、答えは5になります。
この問題は、自由度以外の計算式と必要な値はすべて問題文中に記載されています。
しかしながら自由度の求め方は少しややこしいので、注意が必要です。
No.6の解説は以上です。

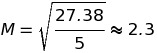
この問題の方向観測の組の数が解らず困ってました。
H26年No6の問題も載せて頂けると幸いです。
コメントありがとうございます。
お役に立てて幸いです。
いただいたご意見のほど、今後検討させていただきます。
私も方向観測の組の数が解らず、こちらのサイトへたどり着きました。解りやすい解説ありがとうございます。これからも解説を参考にさせていただきます。
分かり易い解説有難う御座いました。
ただ一点理解できないのが、方向観察を行っている点の数(合計3つ)という所です。
どこの方向観察なのかご教授頂ければ助かります。
ご質問承りました。
この問題において方向観測(水平角の観測)が行われている点は、
図6における既知点A,B及び新点Eの3点です。
ご質問頂いた記事の箇所は、これらの点を示しております。
早速の返信、誠に有難う御座いました。
α1.2.3.4ありますが、4つではないのですか?
コメントありがとうございます。
返信のほど、遅くなりまして申し訳ございません。
r(方向観測の組の数)についてのご質問でしょうか。
こちらは、記事中にも記載しておりますが、方向観測そのものの数ではなく
方向観測を行っている点の数を示しておりますので、既知点A,B及び新点Eの3つとなります。
ありがとうございます。
ものすごくわかりやすいです。