測量士試験の過去問題を解くシリーズ第3回です。
今回はH27年度午前No.14の問題を解いてみましょう。
[H27-午前No.14 問題]
トータルステーションによる細部測量において,図14に示すとおり,表14-1に示す既知点A,BからTS点Cを設置し,TS点Cから求点Pを観測した。この結果,表14-2及び表14-3の結果を得た。得られた求点PのX座標及びY座標の標準偏差は幾らか。最も近いものの組み合わせを次の中から選べ。
ただし、この測量における距離測定の標準偏差は5mm + 5 × 10^-6D(Dは測定距離),角度の標準偏差は20″であるとし,角度1ラジアンは,2″ × 10^5とする。
なお,関数の数値が必要な場合は,巻末の関数表を使用すること。
X Y
1. 11.0mm 15.4mm
2. 15.4mm 11.0mm
3. 15.5mm 21.5mm
4. 20.7mm 7.7mm
5. 21.5mm 15.5mm
問題文の累乗表記は^で代用しています。また、明記されていませんがDの単位はmです。
そして表は以下。
表14-1
| X座標 | Y座標 | |
| 既知点A | 205.000m | 10.000m |
| 既知点B | 20.000m | 195.000m |
表14-2
| 水平角 | |
| β1 | 345°00′00″ |
| β2 | 120°00′00″ |
表14-3
| 距離 | |
| 既知点A~TS点C | 140.000 |
| TS点C~求点P | 100 |
実はこの問題、選択肢の中に正答がなく試験では全員正解扱いとなりました。正答は
X Y 6. 22.9mm 8.7mm
となります。解答例を挙げるにあたり、最初の一歩は表14-1の値を図14に盛り込み情報を整理することです。こうなります。
次の一歩は表14-2,表14-3の値も図14-1に盛り込み情報を整理することです。最初に盛り込んだ値は既知点由来でるのに対し、ここで盛り込む値は測定値由来で誤差を含む事に注意しましょう。
ごちゃごちゃしますがご容赦を。これで表は用なしです。では、図14-2と
- 距離測定の標準偏差は5mm + 5 × 10^-6D(Dは測定距離(m))
- 角度の標準偏差は20″
から解答を導いていきましょう。
…
この問題、誤差伝播の式を使う以外の方法できっちり解くのはなかなか難しいようです。この式を使って解く場合、偏微分とsin,cosの微分が必要という点が難儀で、出題範囲の広い測量士試験ではそこまで準備の手が回らないという事も多いのではないでしょうか。
まずは誤差伝播の式できっちり解いてみましょう。Aの座標を(ax,ay)(※x,yは添字)、Pの座標を(x,y)と置くと、
と表すことができます。これに対して
を求めて
を代入すれば、それぞれ
となります。また、
s1の標準偏差は5mm + 10^-6 × 140m = 5.7mm
s2の標準偏差は5mm + 10^-6 × 100m = 5.5mm
β1,β2の標準偏差は共に
20″= 20 / (2*10^5) rad = 10^-4rad (radはラジアン)
なので、あとは誤差伝播の式から直接
が導けます。
…
さて、誤差伝播の式を使用した解き方は覚えていれば簡単なのですが、覚えておかなければどうにもなりません。以下は解き方、ではなくて答えの出し方なのですが、試験まで時間がない!偏微分とか蕁麻疹が出る!という場合にどうぞ。
…
まず、CからPを測ったときのPの標準偏差について考えます。
このように、距離測定の標準偏差(誤差と読み替えてもOKです)は青矢印の方向に、角度測定の標準偏差は赤い弧の方向に出ます。
しかし、標準偏差は十分に小さいので上図の赤い弧は直線と思って構いません。両矢印=プラスマイナスもどうでもいいので片側だけにして、
こうなります。
青矢印の長さ(距離測定によるPの標準偏差)は距離測定の標準偏差から
5mm + 5 × 10^-6 × 100m = 5.5mm
20″= 20 / (2*10^5) rad = 10^-4rad (radはラジアン)なので、
赤矢印の長さ(角度測定によるPの標準偏差)は角度測定の標準偏差から
100m × sin(10^-4rad) = 100 × 10^3 × 10^-4 mm = 10mm
です。
さらにX方向とY方向に分解して
こうなります。分解した成分の長さは1/2になったり√3/2になったりですね。
続いてはAからCを測ったときのPの標準偏差を考えなければなりません。PのであってCのではないのが困りものです。
こんな感じで、Cが動くとPにどう影響が出るかを考えなくてはいけません。簡単なのはPにおける距離測定の標準偏差で、これは単純にAからCを測ったときのCの距離測定の標準偏差(青色の矢印)
5mm + 5 × 10^-6 × 140m = 5.7mm
そのものになると予想できます(※1)。平行移動だから、と考えればいいでしょう。X方向とY方向への分解もCで考えたときと同様に行って構いません。問題は角度測定の標準偏差です。
こんな感じで、Aを中心としてPを通る円の、Pでの接線方向に標準偏差が出てしまいます。Cでの標準偏差はX,Yに分解しやすい角度(30°,60°)ですが、APではそうもいきません。
で、Pの標準偏差を考えるのはあきらめて別の都合のよい点で考えます。
こんな風に、「都合のよい」点P’をCPの延長上でAと水平になるように取ります。すると、AからCを測ったときのP’の角度測定の標準偏差は
- AP’を半径とする円のP’での接線方向=垂直方向
に、
- Cでの標準偏差の大きさのAP’/AC倍の大きさ=√3倍
で発生し、微妙な方向を向いていたPの標準偏差(紫の点線矢印)より随分とわかりやすくなります。X方向、Y方向に分解して具体的に値を入れるとこんな状態に。
あとは、CP:CP’=100m:140m=5:7から答えがでると(予想(※2))して、
こうなります。
まとめると
CからPを測ったとき、Pの
距離測定の標準偏差
X 方向 : 2.75mm
Y 方向 : 2.75×√3mm
角度測定の標準偏差
X 方向 : 5×√3mm
Y 方向 : 5mm
AからCを測ったとき、Pの
距離測定の標準偏差
X 方向 : 2.85mm
Y 方向 : 2.85×√3mm
角度測定の標準偏差
X 方向 : 12×√3mm
Y 方向 : 2mm
X 方向 、Y 方向それぞれ二乗和平方根をとれば、
Xの標準偏差
√(2.75^2 + (5×√3)^2 + 2.85^2 + (12×√3 )^2)mm
=√(7.5625 + 75 + 8.1225 + 432)mm
= 22.9mm
Yの標準偏差
√((2.75×√3)^2 + 5^2 + (2.85×√3)^2 + 2^2)mm
=√(22.6875 + 25 + 24.3675 + 4 )mm
= 8.7mm
を求めることができます。
…
さて、正しい解き方と強引に答えだけ弾く方法の2つを紹介しました。後者の方法にせよ、所謂sinx≒xが腑に落ちていたり、最後に標準偏差の二乗和平方根を取ることができたりしなければ答えにたどり着けないので、時間のある方はできるだけ正しい解き方で解答できるよう準備しましょう。
—
※1※2 これらが確信できるなら素直に誤差伝播の式で解くことを推奨。

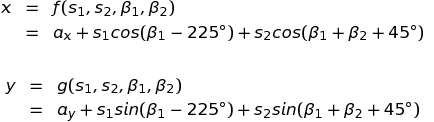

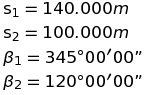
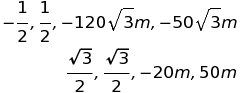
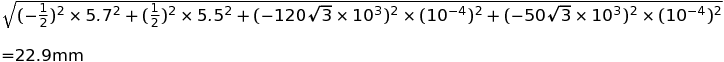


コメント失礼します。
上記の式中に出ている225°というのはどこから導き出された数値なのですか?
答えていただけるとありがたいです。
コメントありがとうございます。
ご質問の225°ですが、これがABから時計回りにx軸の正方向までの角度で、
β1から引くとx軸の正方向から時計回りにACまでの角度(=120°;誤差を含む)になる、
と考えて頂くと分かりやすいかと思います。
図14-2で青の点線と赤の点線が接している点をDとして、
∠DACが60°(=β1-285°)なので…
と解いていってもおそらく同じ答えを出せると思われますので、
是非確かめてみて下さい。
理解できました!
丁寧に答えていただきありがとうございます!
大変わかりやすい解説ありがとうございました。距離の標準偏差5.5mm,5.7mmはすぐにでたのですが、角度の標準偏差で勘違いをしておりました。