測量士試験の過去問題を解くシリーズ、令和2年度試験版の第2回です。

以下、「国土地理院」サイトの 令和2年11月22日の問題を引用して解説して行きます。

〔No.5〕
ある試験において，受験者の点数の平均が60点，標準偏差が10点の結果を得た。受験者の点数の分布が，近似的に平均μ，標準偏差σの正規分布に従うと仮定した場合，80点以上90点以下の人の割合は幾らか。最も近いものを次の中から選べ。ただし，正規分布の性質から，μ±σの範囲に入る確率は68.3％，μ±2σの範囲に入る確率は95.5％，μ± 3σの範囲に入る確率は99.7％とする。なお，関数の値が必要な場合は，巻末の関数表を使用すること。

1.　0.3%
2.　2.1%
3.　2.3%
4.　4.2%
5.　4.5%

正解は2です。下記の2ステップで求めます。

ステップ1
与えられた情報を図にまとめます。

ステップ2
点数が80点以上90点以下の人の割合を求めます。

ステップ1
与えられた情報を図にまとめます。問題で与えられた情報を正規分布のグラフに整理すると、このようになります。

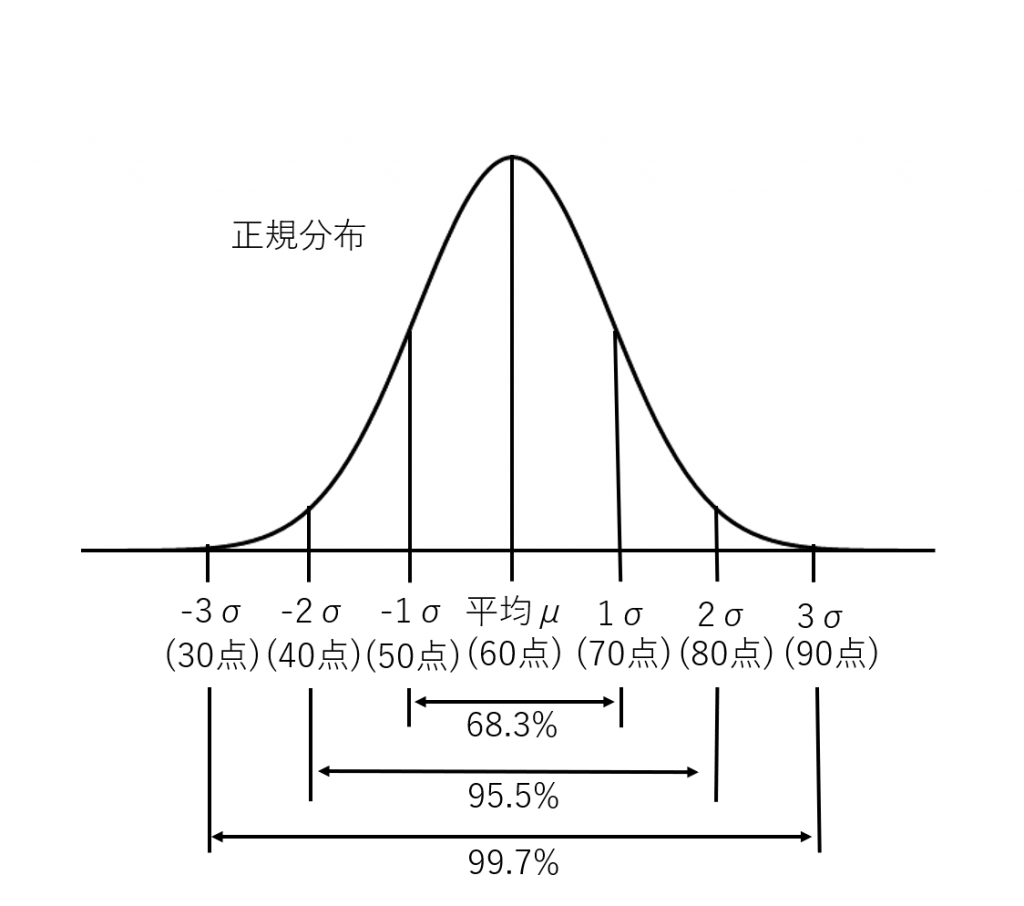
ステップ2
点数が80点以上90点以下の人の割合を求めます。ステップ1の図を確認すると点数が30点以上90点以下の人の割合は99.7%、40点以上80点以下の人の割合は95.5%であることがわかります。このことから点数が30点以上40点以下の人の割合と80点以上90点以下の人の割合の合計は

99.7 – 95.5 = 4.2

4.2%の中で点数が80点以上90点以下の人の割合は半分なので

4.2÷2=2.1

よって点数が80点以上90点以下の人の割合は2の2.1%になります。

測量士試験の過去問題を解くシリーズ、令和2年度試験版の第1回です。

以下、「国土地理院」サイトの 令和2年11月22日の問題を引用して解説して行きます。

〔No．4〕 　
図4に示すような三次元直交座標系において，ある点（x，y，z）をZ軸の周りに図4で示す方向にθ回転させたときの点（x’，y’，z’）の座標は，次の式4で表される。

点P（2.000，－1.000，3.000）をZ軸周りに図4で示す方向に60°回転させたとき，移動後の点P’の座標は，式4より，点P’（1.866，1.232，3.000）となる。この点P’（1.866，1.232，3.000）を，さらにX軸の周りに図4で示す方向に30°回転させたとき，移動後の点P”の座標は幾らか。Z軸周りの回転を表す式4を参考に，X軸周りの回転を表す式を立てて計算し，最も近いものの組合せを次の中から選べ。なお，関数の値が必要な場合は，巻末の関数表を使用すること。

正解は4です。下記の2ステップで求めます。

ステップ1
X軸周りの回転を表す式を求めます。

ステップ2
ステップ1で求めた式を使用して回転後の座標を求めます。

ステップ1
X軸周りの回転を表す式を求めます。 まずは考えやすくするために、図4のX軸を上に向くように回転させます。

与えられた式4は図を変換させる前のZ軸を反時計回りに回転させた式であり、変換後のX軸を反時計回りに回転させた式は次のように変換できます。

ステップ2
ステップ1で求めた式を使用して回転後の座標を求めます。 点P’（1.866，1.232，3.000）をＸ軸周り30°回転させた点P”を求める式は

となります。計算すると、

y” = cos30°×　1.232　+  -sin30°×　3.000　+  0 ×　1.866
 ≒　-0.433
z” = sin30°×　1.232　+   cos30°×　3.000　+  0 ×　1.866
 ≒　3.214
x” = 　0　×　1.232　+ 　0　×　3.000　+　1　×　1.866
 ≒　1.866

よって点P’（1.866，1.232，3.000）をＸ軸周り30°回転させた点P”は4の（1.866、-0.433、3.214）になります。