測量士試験の過去問題を解くシリーズ、令和元年度試験版の第6回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

 〔No．13〕 　　

　視準距離を等しく 45 m として，路線長 1.8 km の水準点Ａ，Ｂ間の水準測量を実施した。1測点に おける1視準1読定の観測の精度（標準偏差）が 0.4 mm であるとき，観測により求められる水準点 Ａ，Ｂ間の片道の観測高低差の精度（標準偏差）は幾らか。最も近いものを次の中から選べ。 　　　
　ただし，1測点では，後視及び前視の観測を1回ずつ，1視準1読定で行ったものとする。
　なお，関数の値が必要な場合は，巻末の関数表を使用すること。 　　

1. 1.0 mm 　　
2. 1.3 mm
3. 1.8 mm
4. 2.5 mm
5. 3.6 mm

（引用終了）

正解は4です。 以下解説して行きます。

何箇所で測定されるかを調べます。
路線長 1.8 km の水準点Ａ，Ｂ間 で、後視及び前視がそれぞれ視準距離45mで行われますので、
S = 1800 ÷ 45 = 40 … ①
40箇所となります。

与えられた 条件から各測定値間の相関はないものとみなせますので、下記の誤差伝搬の法則を適用します。

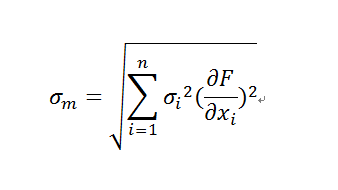
上式の 偏微分の項は全て『1』となります。
１測点に おける１視準１読定の観測 の精度 （標準偏差） は 『0.4』 と与えられているため、 全ての δi は 0.4となります。
上記①から、n = 40となります。
よって、各々の値を代入すると下記の様になります。

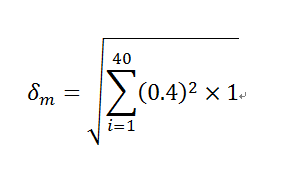
よって、
δｍ =√(40 ×(0.4 ×0.4)) ≒ 2.53
となります。
　　　　　　　　　　　　　　　
最も近い値は2.5ですので、解答は4となります。

以上です。

測量士試験の過去問題を解くシリーズ、令和元年度試験版の第5回です。

以下、「国土地理院」サイトの 令和元年5月19日の問題を引用して解説して行きます。

[R 1-午前No.10問題] （以下引用開始）

 〔No．10〕

　既知点Ａ及び新点Ｂにおいて GNSS 測量機を用いた測量を行い，既知点Ａから新点Ｂまでの楕円体 面上の距離 8,000.00 m，新点Ｂの楕円体高 65.40 m の値を得た。このとき，新点Ｂの標高は幾らか。最 も近いものを次の中から選べ。 　 　ただし，既知点Ａの標高は 45.00 m，楕円体高は 83.00 m であり，ジオイドは，楕円体面に対し既知 点Ａから新点Ｂの方向へ，楕円体面上の距離 1,000.00 m 当たり－0.02 m で一様に傾斜しているものと する。 なお，関数の値が必要な場合は，巻末の関数表を使用すること。 　　

1. 　27.14 m 　　
2. 　27.24 m 　　
3. 　27.40 m
4. 　27.56 m
5. 　28.56 m

（引用終了）

正解は4です。 以下解説して行きます。

ジオイドとは、 国土地理院サイト (https://www.gsi.go.jp/) から
(以下引用開始）

水は、高いところから低いところに流れます。地図に記される高さ（標高）は、水道などのインフラ整備や、津波や洪水等から命を守る上でとても大切な情報ですが、実はその標高は地形の起伏だけでは決められません。平らに見える地表面でも、重力の分布が一様でなければ、水は重力の強い方に流れています。同じように、正確な標高を知るためには、地形の起伏を測定するだけではなく、重力の影響も考慮する必要があります。

　日本の標高の基準は、測量法で平均海面と定められています。この平均海面を仮想的に陸地へ延長した面をジオイドといいます。
　国土地理院では、重力測量や水準測量の結果などから、地球を仮想的に表した楕円体表面からジオイドまでの高さ（ジオイド高）を決めています。衛星測位で決まる高さ（楕円体高）からジオイド高を引くことで、簡単に標高を求めることができます。

（引用終了）

問を図示すると下記のようになります。

流れとして、図のAgを求めてBgを求めて、Xを求めます。

既知点Aのジオイド高:Agを求めます。
Ag=83.00m-45.00m
=38.00m

新点Bのジオイド高:Bgを求めます。
Bg=Ag+(8000.00m÷1000.00m)×(-0.02)
=38.00m-0.16
=37.84m

新点Bの標高:Xを求めます。
X=65.40m-Bg
=65.40m-37.84m
=27.56m

という事で、解答は４番となります。

以上です。